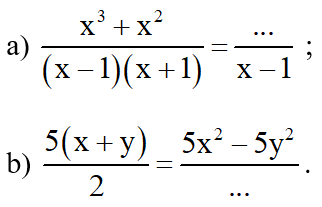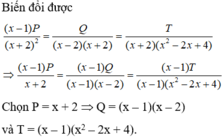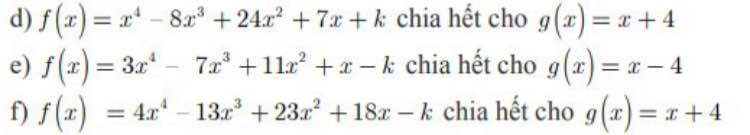Giúp em vs.Em cần gấp.Cảm ơn trc ạ
Bài 1:
\(a,VT=\dfrac{3x-1}{\left(x+2\right)\left(3x-1\right)}=\dfrac{1}{x+2}=VP\\ b,VT=\dfrac{x^2+2x+4}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{1}{x-2}\\ VP=\dfrac{x+3}{\left(x+3\right)\left(x-2\right)}=\dfrac{1}{x-2}\\ \Rightarrow VT=VP\\ c,VT=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{2\left(x-2\right)}=\dfrac{x^2+2x+4}{2}=VP\)
Bài 2:
\(a,A=\dfrac{\left(x-4\right)\left(x+4\right)}{x-4}=x+4=2019+4=2023\\ b,2x-1=0\Leftrightarrow x=\dfrac{1}{2}\\ B=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x-2\right)}=\dfrac{2x}{x-2}=\dfrac{2\cdot\dfrac{1}{2}}{\dfrac{1}{2}-2}=\dfrac{1}{-\dfrac{3}{2}}=-\dfrac{2}{3}\\ c,x^2-9=0\Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-3\left(tm\right)\end{matrix}\right.\Leftrightarrow x=-3\\ P=\dfrac{x-3}{\left(x-3\right)\left(x-2\right)}=\dfrac{1}{x-2}=\dfrac{1}{-3-2}=-\dfrac{1}{5}\)
Bài 3:
\(a,A=\dfrac{2\left(2x-3\right)}{2x^2-7x+6}=\dfrac{2\left(2x-3\right)}{\left(x-2\right)\left(2x-3\right)}=\dfrac{2}{x-2}\\ b,A=\dfrac{\left(x^2+2x\right)\left(2x^2-3x-2\right)}{x^2-2x}=\dfrac{x\left(x+2\right)\left(x-2\right)\left(2x+1\right)}{x\left(x-2\right)}=\left(x+2\right)\left(2x+1\right)\)
