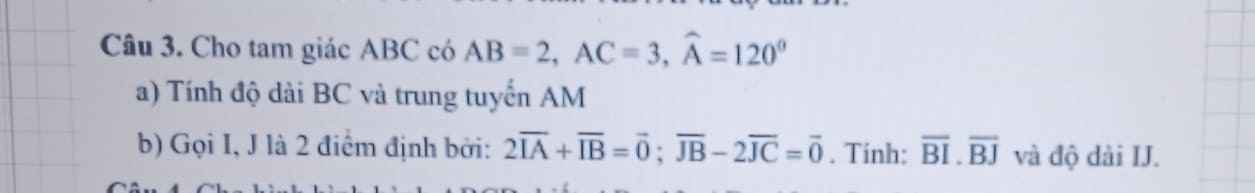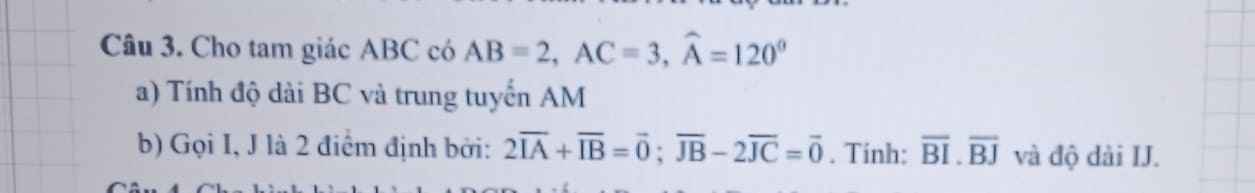a.
Áp dụng định lý hàm cos:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=\sqrt{19}\)
Áp dụng công thức trung tuyến:
\(AM=\sqrt{\dfrac{2\left(AB^2+AC^2\right)-BC^2}{4}}=\dfrac{\sqrt{7}}{2}\)
b.
\(2\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\Leftrightarrow2\overrightarrow{IB}+2\overrightarrow{BA}+\overrightarrow{IB}=\overrightarrow{0}\Leftrightarrow\overrightarrow{IB}=\dfrac{2}{3}\overrightarrow{AB}\Rightarrow\overrightarrow{BI}=-\dfrac{2}{3}\overrightarrow{AB}\)
\(\overrightarrow{JB}-2\overrightarrow{JC}=\overrightarrow{0}\Rightarrow\overrightarrow{JB}=2\overrightarrow{JC}=2\overrightarrow{JB}+2\overrightarrow{BC}\Rightarrow\overrightarrow{JB}=-2\overrightarrow{BC}\Rightarrow\overrightarrow{BJ}=2\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BI}.\overrightarrow{BJ}=-\dfrac{2}{3}\overrightarrow{AB}.2\overrightarrow{BC}=-\dfrac{4}{3}\overrightarrow{AB}.\overrightarrow{BC}=-\dfrac{4}{3}\overrightarrow{AB}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{4}{3}AB^2-\dfrac{4}{3}\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{4}{3}.2^2-\dfrac{4}{3}.2.3.cosA=\dfrac{28}{3}\)
Độ dài IJ:
Ta có: \(\overrightarrow{BI}=-\dfrac{2}{3}\overrightarrow{AB}\Rightarrow BI=\dfrac{2}{3}AB=\dfrac{4}{3}\)
\(\overrightarrow{BJ}=2\overrightarrow{BC}\Rightarrow BJ=2BC=2\sqrt{19}\)
Từ đó:
\(IJ^2=\overrightarrow{IJ}^2=\left(\overrightarrow{IB}+\overrightarrow{BJ}\right)^2=IB^2+BJ^2+2\overrightarrow{IB}.\overrightarrow{BJ}\)
\(=IB^2+BJ^2-2\overrightarrow{BI}.\overrightarrow{BJ}\)
\(=\left(\dfrac{4}{3}\right)^2+\left(2\sqrt{19}\right)^2-2.\dfrac{28}{3}=...\)