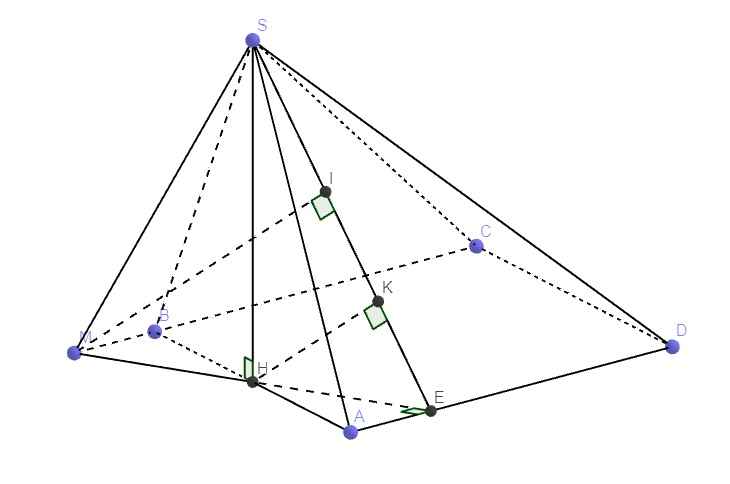
Kẻ \(HE\perp AD\) , do tam giác ABD đều \(\Rightarrow HE=\dfrac{a\sqrt{3}}{2}\) ; \(AE=\dfrac{1}{4}AD\)
\(\Rightarrow AE=BM\Rightarrow\) tứ giác AEBM là hình bình hành \(\Rightarrow\) H đồng thời là trung điểm ME
Kẻ \(HK\perp SE\Rightarrow HK\perp\left(SAD\right)\)
a. Ta có: \(SH=HE\Rightarrow\) tam giác SHE vuông cân tại H
\(\Rightarrow\) K đồng thời là trung điểm SE
\(\Rightarrow\) KH là đường trung bình tam giác SME \(\Rightarrow SM||HK\)
\(\Rightarrow SM\perp\left(SAD\right)\)
b. Từ C kẻ \(CX\perp\left(SAD\right)\Rightarrow\widehat{CSX}\) là góc giữa SC và (SAD) đồng thời \(CX=d\left(C;\left(SAD\right)\right)\)
\(\Rightarrow sin\alpha=sin\widehat{CSX}=\dfrac{CX}{SC}\)
Từ M kẻ \(MI\perp SE\Rightarrow MI||HK\Rightarrow MI\perp\left(SAD\right)\)
\(\Rightarrow MI=d\left(M;\left(SAD\right)\right)\)
Mà \(CM||AD\Rightarrow CM||\left(SAD\right)\Rightarrow d\left(C;\left(SAD\right)\right)=d\left(M;\left(SAD\right)\right)\)
\(\Rightarrow CX=MI\)
HK là đường trung bình tam giác MIE \(\Rightarrow MI=2HK\)
\(MI=2HK=\dfrac{2SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{SH.a\sqrt{3}}{\sqrt{SH^2+\dfrac{3a^2}{4}}}\)
\(SC=\sqrt{SH^2+CH^2}=\sqrt{SH^2+MH^2+CM^2}=\sqrt{SH^2+HE^2+CM^2}\)
\(=\sqrt{SH^2+7a^2}\)
\(\Rightarrow sin\alpha=\dfrac{SH.a\sqrt{3}}{\sqrt{SH^2+7a^2}.\sqrt{SH^2+\dfrac{3a^2}{4}}}=\dfrac{a\sqrt{3}}{\sqrt{SH^2+\dfrac{21a^4}{4SH^2}+\dfrac{31}{4}a^2}}\le\dfrac{a\sqrt{3}}{\sqrt{2\sqrt{\dfrac{21a^4}{4}}+\dfrac{31}{4}a^2}}\)
Dấu "=" xảy ra khi \(SH^2=\dfrac{21a^4}{4SH^2}\Rightarrow SH=a\sqrt[4]{\dfrac{21}{4}}\)
Em kiểm tra lại tính toán

 giúp em với em cảm ơn nhiều lắmmm ạ
giúp em với em cảm ơn nhiều lắmmm ạ