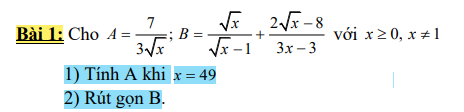Bài 1:
1: Thay x=49 vào A, ta được:
\(A=\dfrac{7}{3\cdot7}=\dfrac{1}{3}\)
2: \(B=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2\sqrt{x}-8}{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)+2\sqrt{x}-8}{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+5\sqrt{x}-8}{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}+8}{3\left(\sqrt{x}+1\right)}\)
1) Ta có A khi x = 49 :
\(A=\dfrac{7}{3\sqrt{49}}=\dfrac{7}{21}=\dfrac{1}{3}\)
Vậy khi x = 49 thì \(A=\dfrac{1}{3}\)
2)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2\sqrt{x}-8}{3x-3}\left(x\ge0;x\ne1\right)\\ =\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2\sqrt{x}-8}{3\left(x-1\right)}\\ =\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)+2\sqrt{x}-8}{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{3x+3\sqrt{x}+2\sqrt{x}-8}{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{3x+5\sqrt{x}-8}{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{3\sqrt{x}+8}{3\left(\sqrt{x}+1\right)}\)