a) \(x^2-3x=0\)
\(x\left(x-3\right)=0\)
⇔\(\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
b) \(5x^3-15x^2=0\)
\(5x^2\left(x-3\right)=0\)
⇔\(\left[{}\begin{matrix}5x^2=0\\x-3=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
\(a,\Rightarrow x\left(x-3\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\\ b,\Rightarrow2x\left(1-2x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\\ c,\Rightarrow5x^2\left(x-3\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\\ d,\Rightarrow x\left(x^2-9\right)=0\\ \Rightarrow x\left(x-3\right)\left(x+3\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
c) \(2x-4x^2=0\)
\(2x\left(1-2x\right)=0\)
⇔\(\left[{}\begin{matrix}2x=0\\1-2x=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
d) \(x^3-9x=0\)
\(x\left(x^2-9\right)=0\)
\(x\left(x^2-3^2\right)=0\)
\(x\left(x+3\right)\left(x-3\right)=0\)
⇔\(\left[{}\begin{matrix}x=0\\x+3=0\\x-3=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=-3\\x=3\end{matrix}\right.\)

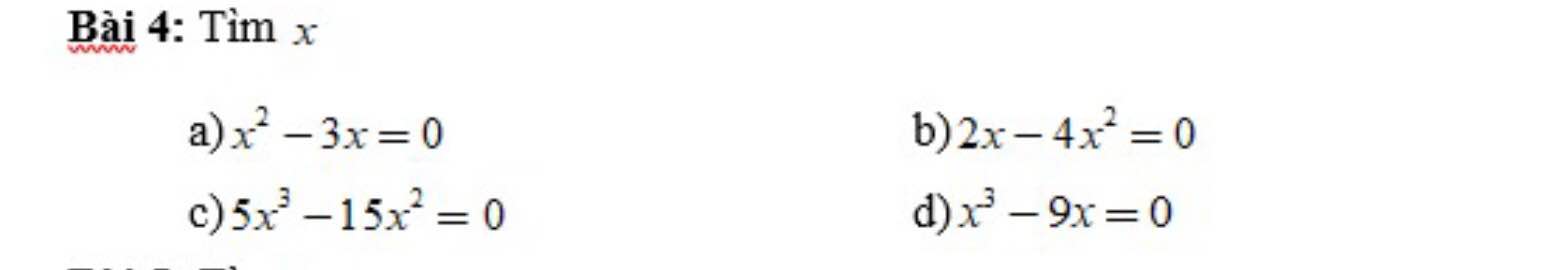 giúp em với :3
giúp em với :3








 giúp em nhé các anh chị :3
giúp em nhé các anh chị :3


