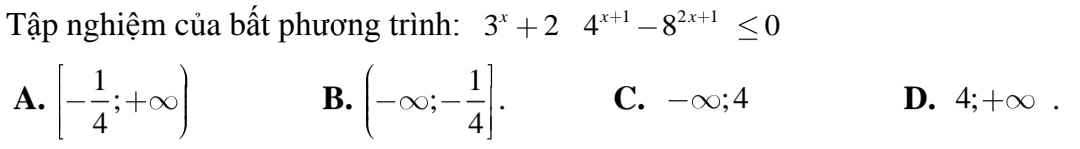\(\dfrac{2020}{2019}>\dfrac{2019}{2020}\Rightarrow0< a< 1\)
\(log_ba< 1\Rightarrow b>1\)
\(P=log_b^2a+log_b^22-\dfrac{m^2log_2b}{log_2a}+2\left(log_ba-2log_b2\right)-\dfrac{4^{ab^2}-2m.2^{ab^2}}{log_ba}\)
\(=log_b^2a+log_b^22+2log_ba-4log_b2-\dfrac{4^{ab^2}-2m.2^{ab^2}+m^2}{log_ba}\)
\(=\left(log_ba+1\right)^2+\left(log_b2-2\right)^2+\dfrac{\left(2^{ab^2}-m\right)^2}{-log_ba}-5\ge-5\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}log_ba=-1\\log_b2=2\\2^{ab^2}=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{2}}\\b=\sqrt{2}\\m=2^{ab^2}=2^{\sqrt{2}}\end{matrix}\right.\)
Sau khi tính lại thì không có đáp án nào đúng :(