a)
\(=2y\left(10y-3\right)+15\left(10y-3\right)\\ =\left(10y-3\right)\left(2y+15\right)\)
b)
\(=3x\left(x-7y\right)-24\left(x-7y\right)\\ =\left(x-7y\right)\left(3x-24\right)\)
\(=3\left(x-7y\right)\left(x-8\right)\)
c)
\(=21x\left(4x+5\right)+9\left(4x+5\right)\\ =\left(4x+5\right)\left(21x+9\right)\\ =3\left(4x+5\right)\left(7x+3\right)\)
d)
\(=12\left(x-5\right)+5y\left(5-x\right)\\ =12\left(x-5\right)-5y\left(x-5\right)\\ =\left(x-5\right)\left(12-5y\right)\)
e)
\(=5x\left(2y-z\right)+x^2\left(2y-z\right)\\ =\left(2y-z\right)\left(5x+x^2\right)\\ =x\left(2y-z\right)\left(5+x\right)\)
f)
\(=2xy\left(y-3z\right)-10x\left(3z-y\right)\\ =2xy\left(y-3z\right)+10x\left(y-3z\right)\\ =\left(y-3z\right)\left(2xy+10x\right)\\ =2x\left(y-3z\right)\left(y+5\right)\)
`HaNa☘D`
a) \(2y\left(10y-3\right)-15\left(3-10y\right)\)
\(=2y\left(10y-3\right)+15\left(10y-3\right)\)
\(=\left(10y-3\right)\left(2y-15\right)\)
b) \(3x\left(x-7y\right)+24\left(7y-x\right)\)
\(=3x\left(x-7y\right)-24\left(x-7y\right)\)
\(=3\left(x-7y\right)\left(x-8\right)\)
c) \(21x\left(4x+5\right)+36x+45\)
\(=21x\left(4x+5\right)+9\left(4x+5\right)\)
\(=3\left(7x+3\right)\left(4x+5\right)\)
d) \(12x-60+5y\left(5-x\right)\)
\(=12\left(x-5\right)-5y\left(x-5\right)\)
\(=\left(x-5\right)\left(12-5y\right)\)
e) \(5x\left(2y-z\right)+2x^2y+x^2z\)
\(=5x\left(2y-z\right)+x^2\left(2y+z\right)\)
\(=x\left(x+5\right)\left(2y-z\right)\)
f) \(2xy^2-6xyz-10x\left(3z-y\right)\)
\(=2xy\left(y-3z\right)+10x\left(y-3z\right)\)
\(=2x\left(y-3z\right)\left(y+5\right)\)












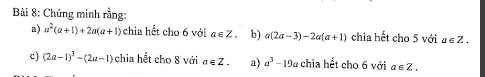



 Giúp em câu này vs ạ
Giúp em câu này vs ạ
