a: Tọa độ đỉnh của (P) là:
\(\left\{{}\begin{matrix}x=\dfrac{-3}{2\cdot\left(-1\right)}=\dfrac{3}{2}\\y=-\dfrac{3^2-4\cdot\left(-1\right)\cdot\left(-2\right)}{4\cdot\left(-1\right)}=-\dfrac{9-4\cdot2}{-4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{9-8}{4}=\dfrac{1}{4}\end{matrix}\right.\)
Vì (P): \(y=-x^2+3x-2\) có a=-1<0
nên hàm số đồng biến trên khoảng \(\left(-\infty;\dfrac{3}{2}\right)\) và nghịch biến trên khoảng \(\left(\dfrac{3}{2};+\infty\right)\)
Bảng biến thiên là:

Đồ thị là:
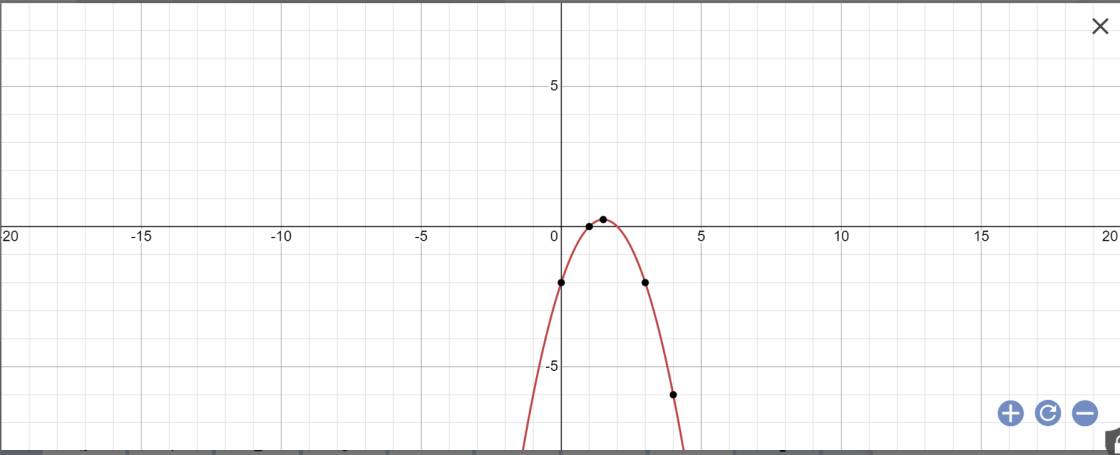
b: Dựa vào đồ thị, ta sẽ có:
Để y>0 thì 1<x<2
c: \(x^2-3x-m=0\)
=>\(x^2-3x=m\)
=>\(-x^2+3x=-m\)
=>\(-x^2+3x-2=2-m\)
Đặt \(y=g\left(x\right)=-x^2+3x-2\)
\(\Leftrightarrow y'=g'\left(x\right)=-2x+3\)
Đặt g'(x)=0
=>-2x+3=0
=>\(x=\dfrac{3}{2}\)
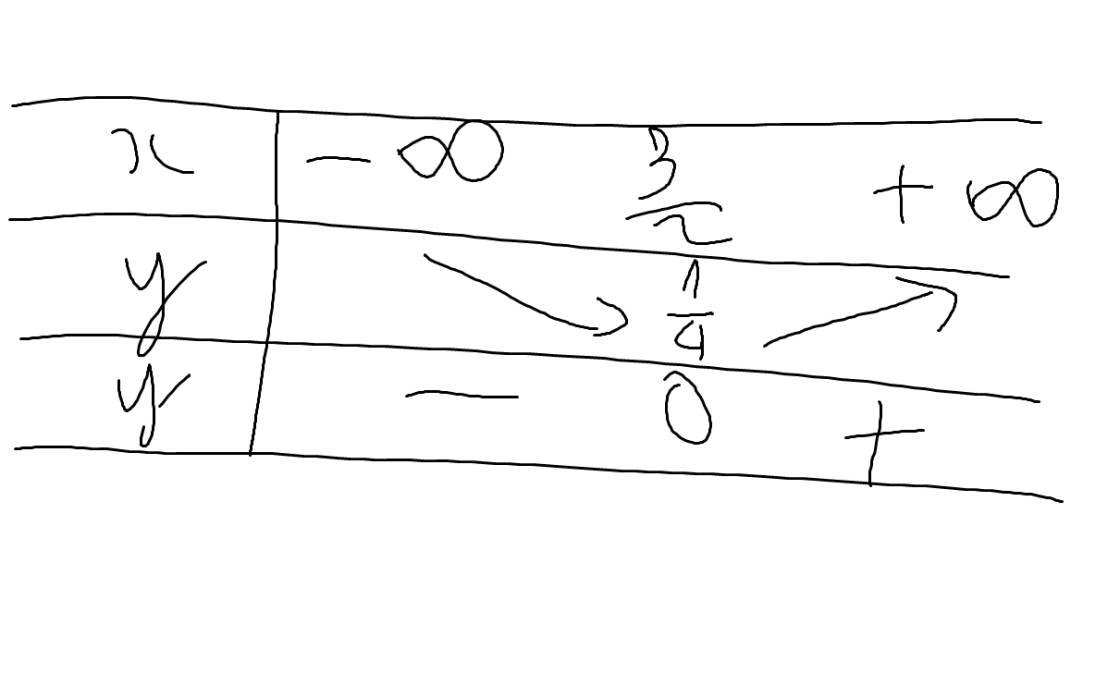
Để phương trình có 1 nghiệm thì \(2-m=\dfrac{1}{4}\)
=>\(m=2-\dfrac{1}{4}=\dfrac{7}{4}\)
Để phương trình có hai nghiệm thì \(2-m\ne\dfrac{1}{4}\)
=>\(m\ne2-\dfrac{1}{4}=\dfrac{7}{4}\)