\(D=R\backslash\left\{1\right\}\)
\(y'=\dfrac{x\left(x-2\right)}{\left(x-1\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x^2+2x-2}{x-1}=-\infty\) ; \(\lim\limits_{x\rightarrow+\infty}\dfrac{x^2+2x-2}{x-1}=+\infty\)
\(\lim\limits_{x\rightarrow1^-}\dfrac{x^2+2x-2}{x-1}=-\infty\) ; \(\lim\limits_{x\rightarrow1^+}\dfrac{x^2+2x-2}{x-1}=+\infty\)
Bảng biến thiên:
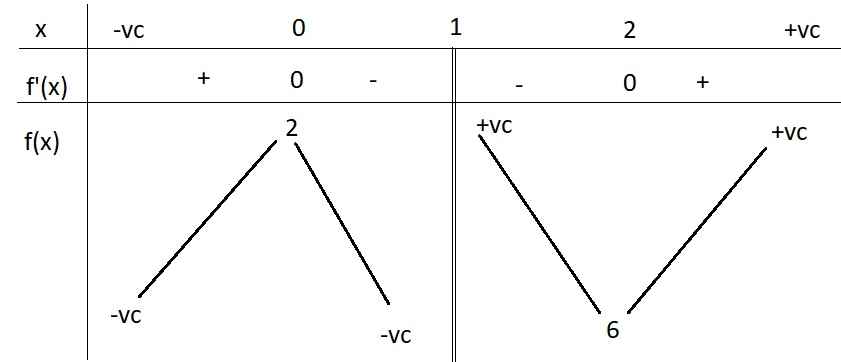
Hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(0;1\right)\) và \(\left(1;2\right)\)
\(x=0\) là điểm cực đại, \(x=6\) là điểm cực tiểu
Đồ thị em tự vẽ
b.
\(x^2+\left(2-m\right)x+m-2=0\Leftrightarrow x^2+2x-2=m\left(x-1\right)\)
- Với \(x=1\) không là nghiệm
- Với \(x\ne1\Rightarrow m=\dfrac{x^2+2x-2}{x-1}\)
Từ đồ thị (hay BBT) ta thấy:
- Phương trình có 2 nghiệm pb khi \(\left[{}\begin{matrix}m>6\\m< 2\end{matrix}\right.\)
- Phương trình có nghiệm kép khi \(\left[{}\begin{matrix}m=6\\m=2\end{matrix}\right.\)
- Phương trình vô nghiệm khi \(2< m< 6\)















