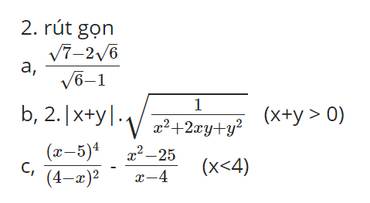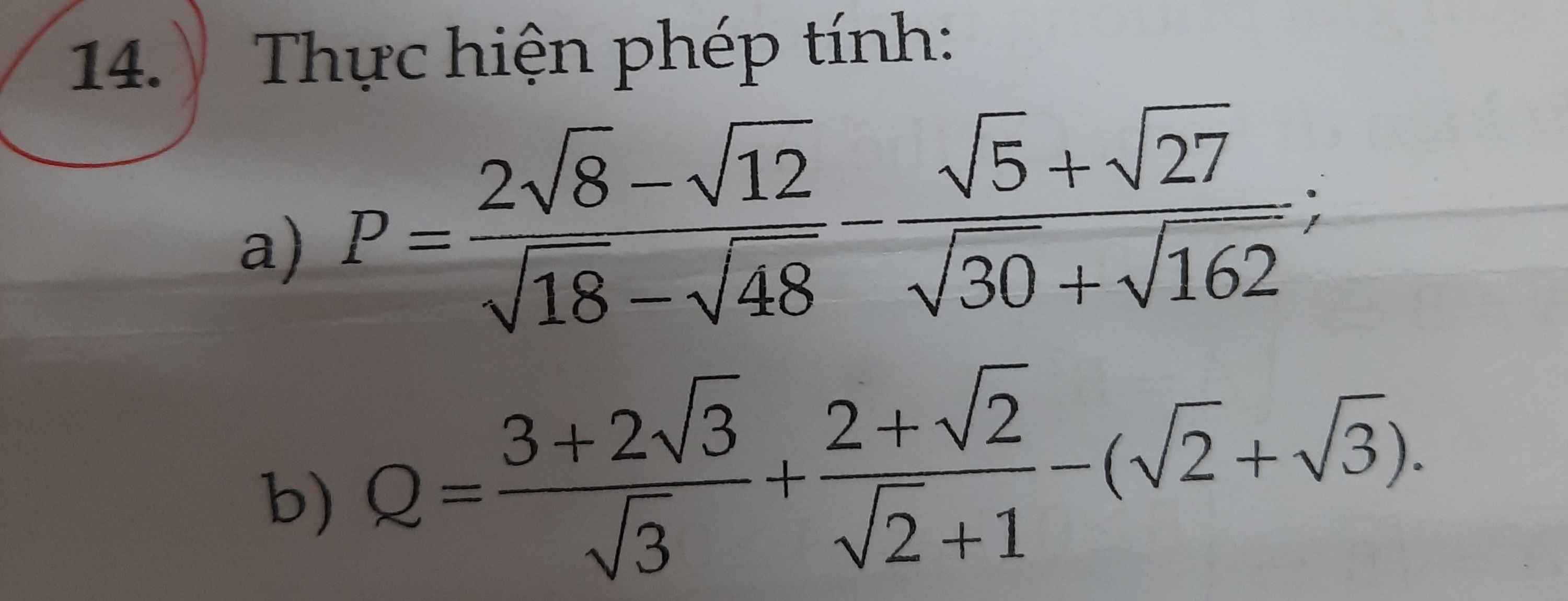Bài 5:
a: \(A=\sqrt{12-3\sqrt7}-\sqrt{12+3\sqrt7}\)
\(=\frac{1}{\sqrt2}\left(\sqrt{24-6\sqrt7}-\sqrt{24+6\sqrt7}\right)\)
\(=\frac{1}{\sqrt2}\cdot\left(\sqrt{21-2\cdot\sqrt{21}\cdot\sqrt3+3}-\sqrt{21+2\cdot\sqrt{21}\cdot\sqrt3+3}\right)\)
\(=\frac{1}{\sqrt2}\left(\sqrt{\left(\sqrt{21}-\sqrt3\right)^2}-\sqrt{\left(\sqrt{21}+\sqrt3\right)^2}\right)\)
\(=\frac{1}{\sqrt2}\left(\sqrt{21}-\sqrt3-\sqrt{21}-\sqrt3\right)=\frac{1}{\sqrt2}\cdot\left(-2\sqrt3\right)=-\sqrt6\)
b: \(B=\sqrt{4+\sqrt{10+2\sqrt5}}+\sqrt{4-\sqrt{10+2\sqrt5}}\)
=>\(B^2=4+\sqrt{10+2\sqrt5}+4-\sqrt{10+2\sqrt5}+2\cdot\sqrt{\left(4+\sqrt{10+2\sqrt5}\right)\left(4-\sqrt{10+2\sqrt5}\right)}\)
=>\(B^2=8+2\cdot\sqrt{16-\left(10+2\sqrt5\right)}=8+2\cdot\sqrt{6-2\sqrt5}\)
=>\(B^2=8+2\left(\sqrt5-1\right)=6+2\sqrt5\)
=>\(B^2=\left(\sqrt5+1\right)^2\)
=>\(B=\sqrt5+1\)
c: \(C=\sqrt{3-\sqrt5}+\sqrt{3+\sqrt5}\)
\(=\frac{1}{\sqrt2}\left(\sqrt{6-2\sqrt5}+\sqrt{6+2\sqrt5}\right)\)
\(=\frac{1}{\sqrt2}\left(\sqrt{\left(\sqrt5-1\right)^2}+\sqrt{\left(\sqrt5+1\right)^2}\right)\)
\(=\frac{1}{\sqrt2}\left(\sqrt5-1+\sqrt5+1\right)=\frac{1}{\sqrt2}\cdot2\sqrt5=\sqrt{10}\)
Bài 4:
a: \(\frac{10+2\sqrt{10}}{\sqrt5+\sqrt2}+\frac{8}{1-\sqrt5}\)
\(=\frac{\sqrt{100}+\sqrt{40}}{\sqrt5+\sqrt2}-\frac{8\left(\sqrt5+1\right)}{\left(\sqrt5+1\right)\left(\sqrt5-1\right)}\)
\(=\frac{2\sqrt5\left(\sqrt5+\sqrt2\right)}{\sqrt5+\sqrt2}-2\left(\sqrt5+1\right)=2\sqrt5-2\sqrt5-2=-2\)
b: \(\frac{2\sqrt8-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\frac{\sqrt5+\sqrt{27}}{\sqrt{30}+\sqrt{162}}\)
\(=\frac{2\left(\sqrt8-\sqrt3\right)}{\sqrt6\left(\sqrt8-\sqrt3\right)}-\frac{\sqrt5+\sqrt7}{\sqrt6\left(\sqrt5+\sqrt7\right)}=\frac{2}{\sqrt6}-\frac{1}{\sqrt6}=\frac{1}{\sqrt6}=\frac{\sqrt6}{6}\)
c: \(\sqrt{\frac{2-\sqrt3}{2+\sqrt3}}+\sqrt{\frac{2+\sqrt3}{2-\sqrt3}}\)
\(=\sqrt{\frac{\left(2-\sqrt3\right)\left(2-\sqrt3\right)}{\left(2+\sqrt3\right)\left(2-\sqrt3\right)}}+\sqrt{\frac{\left(2+\sqrt3\right)\left(2+\sqrt3\right)}{\left(2-\sqrt3\right)\left(2+\sqrt3\right)}}\)
\(=\sqrt{\left(2-\sqrt3\right)^2}+\sqrt{\left(2+\sqrt3\right)^2}\)
\(=2-\sqrt3+2+\sqrt3=4\)
d: \(\frac{\sqrt{3-\sqrt5}\left(3+\sqrt5\right)}{\sqrt{10}+\sqrt2}\)
\(=\frac{\sqrt{6-2\sqrt5}\left(3+\sqrt5\right)}{2\left(\sqrt5+1\right)}=\frac{\sqrt{\left(\sqrt5-1\right)^2}\cdot\left(3+\sqrt5\right)}{2\left(\sqrt5+1\right)}\)
\(=\frac{\left(\sqrt5-1\right)\left(3+\sqrt5\right)}{2\left(\sqrt5+1\right)}=\frac{3\sqrt5+5-3-\sqrt5}{2\left(\sqrt5+1\right)}=\frac{2+2\sqrt5}{2+2\sqrt5}=1\)
f: \(\frac{\left(\sqrt5+2\right)^2-8\sqrt5}{2\sqrt5-4}=\frac{9+4\sqrt5-8\sqrt5}{2\sqrt5-4}\)
\(=\frac{9-4\sqrt5}{2\left(\sqrt5-2\right)}=\frac{\left(\sqrt5-2\right)^2}{2\left(\sqrt5-2\right)}=\frac{\sqrt5-2}{2}\)