Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{2b}=\dfrac{b}{2c}=\dfrac{c}{2d}=\dfrac{d}{2a}=\dfrac{a+b+c+d}{2a+2b+2c+2d}=\dfrac{a+b+c+d}{2\left(a+b+c+d\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{2b}{2}=b\\b=\dfrac{2c}{2}=c\\c=\dfrac{2d}{2}=d\\d=\dfrac{2a}{2}=a\end{matrix}\right.\)\(\Rightarrow a=b=c=d\)
Ta có:
\(A=\dfrac{2011a-2010b}{c+d}+\dfrac{2011b-2010c}{a+d}+\dfrac{2011c-2010d}{a+b}+\dfrac{2011d-2010a}{b+c}\)
\(\Rightarrow A=\dfrac{2011a-2010a}{a+a}+\dfrac{2011a-2010a}{a+a}+\dfrac{2011a-2010a}{a+a}+\dfrac{2011a-2010a}{a+a}\)
\(\Rightarrow A=\dfrac{a}{a+a}+\dfrac{a}{a+a}+\dfrac{a}{a+a}+\dfrac{a}{a+a}\)
\(\Rightarrow A=\dfrac{a+a+a+a}{2a}=\dfrac{4a}{2a}=2\)
Vậy \(A=2\)
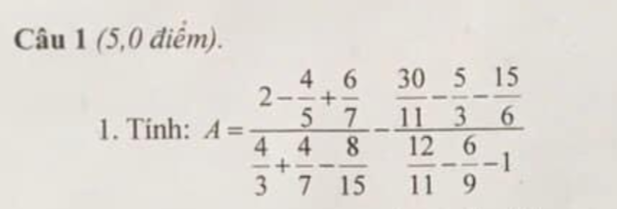
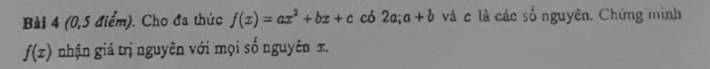giúp e ạ
giúp em vs ạ
Ai ai giúp với Ạ!