Ta có:\(Q=\frac{2x^3+x^2+2x+8}{2x+1}=\frac{2x^3+x^2}{2x+1}+\frac{2x+1}{2x+1}+\frac{7}{2x+1}\)
\(=x^2+1+\frac{7}{2x+1}\)
Để Q là số nguyên thì:\(2x+1\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
| \(2x+1\) | \(1\) | \(\)\(-1\) | \(7\) | \(-7\) |
| \(x\) | \(0\) | \(-1\) | \(3\) | \(-4\) |
Vậy để Q nguyên thì \(x\in\left\{-4;-1;0;3\right\}\)\(\)
ta phân tích 2x^3+x^2+2x+8 ra nhé
<=>(x^2+1).(2x+1)+7 (đảm bảo giá trị ban đầu nhé)
thay vào biểu thức ta có
(x^2+1)(2x+1)+7/2x+1
<=>(x^2+1).(2x+1)/2x+1+7/2x+1
<=>x^2+1+7/2x+1
còn lại làm như bạn Bình Dị nhé
giúp câu 2
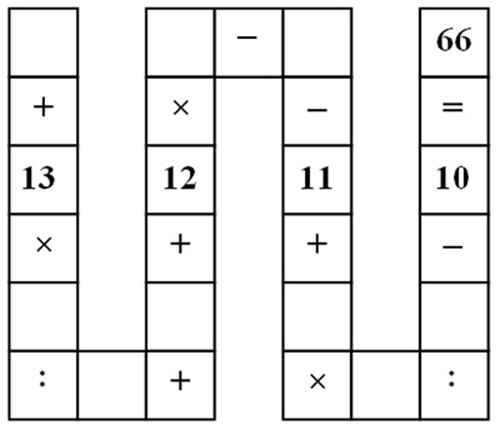
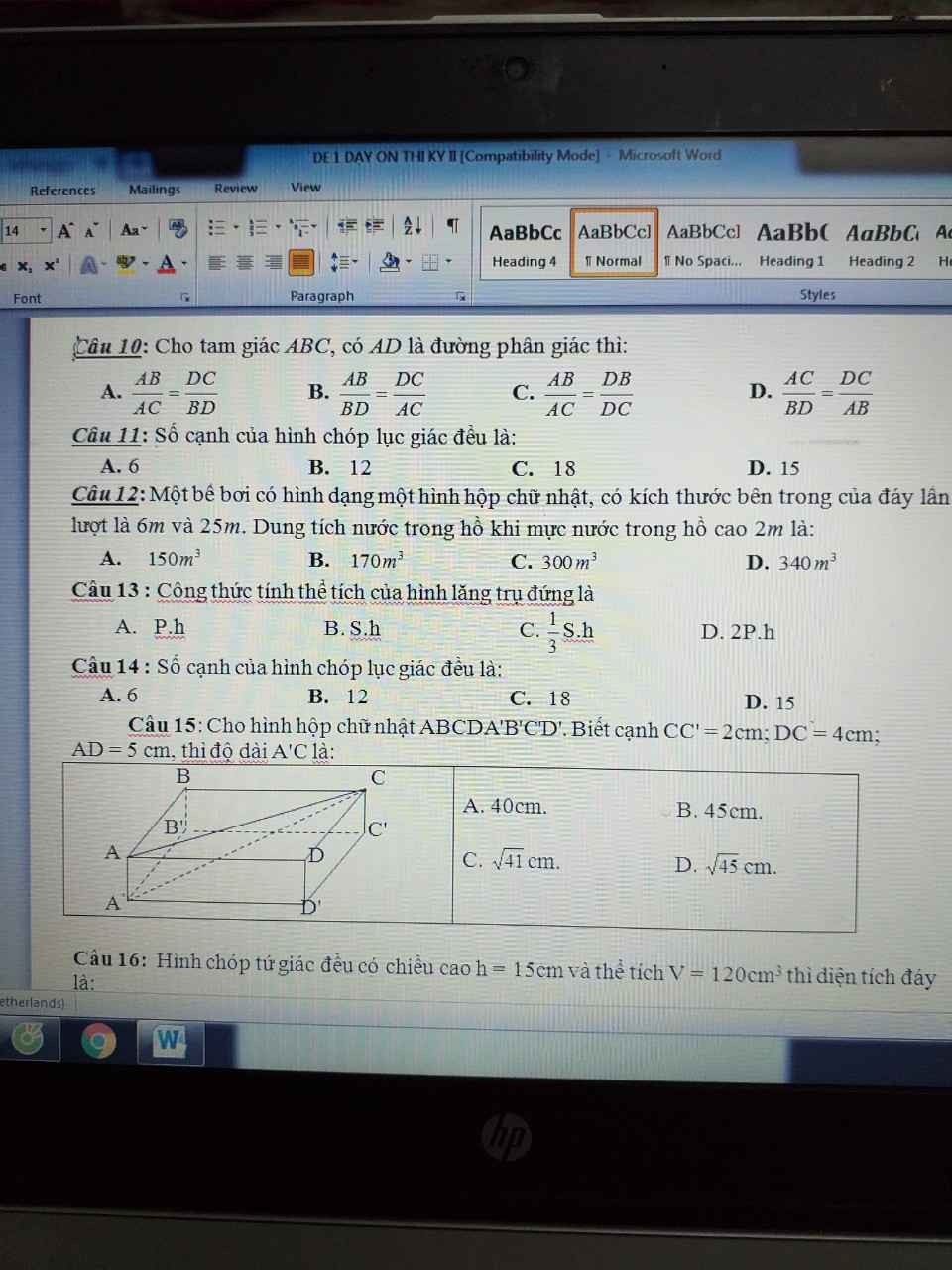
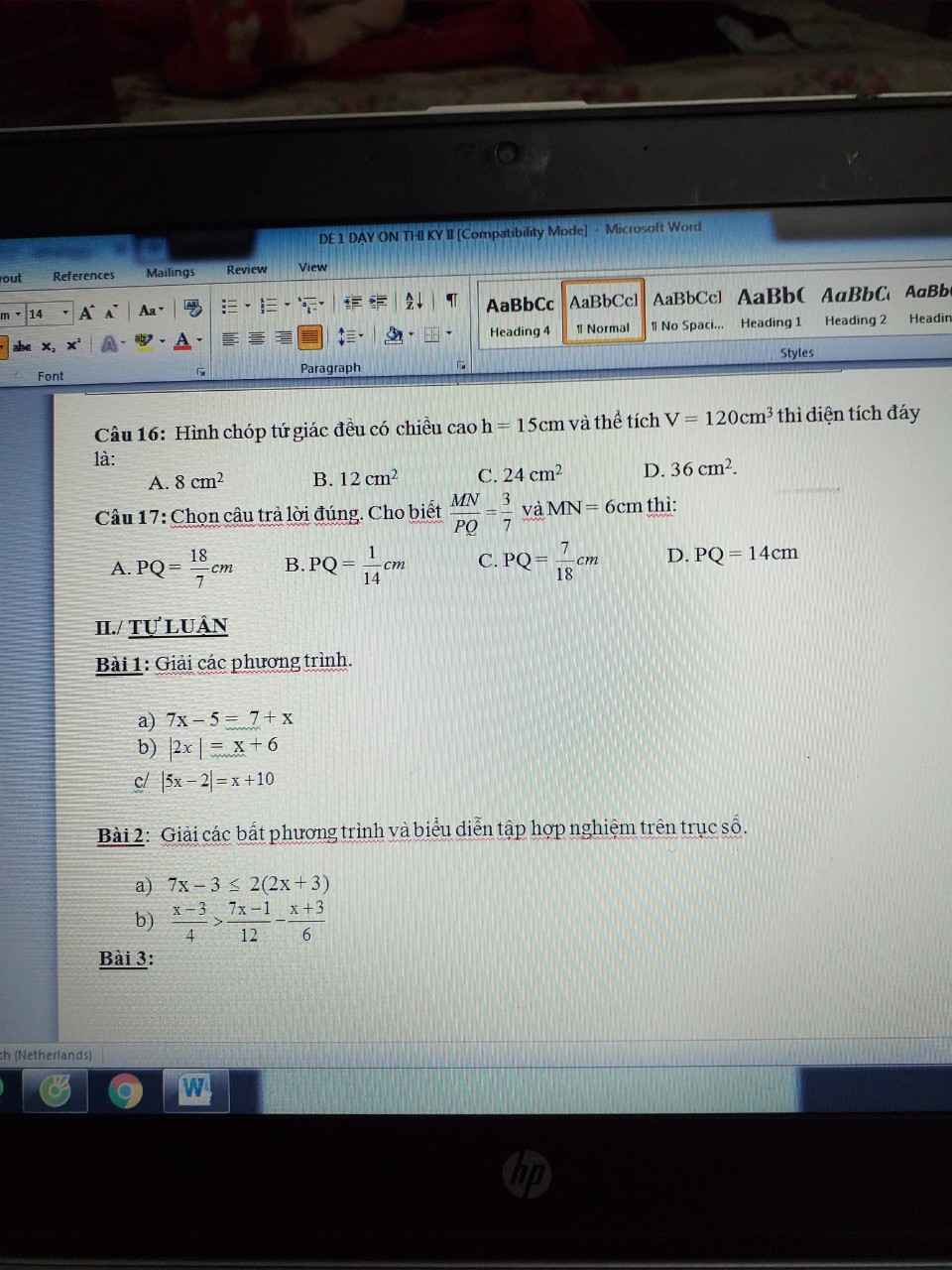
úp mình câu này với ạ <3 
