Lời giải:
\(A=\frac{1}{4}+\frac{1}{4^2}+....+\frac{1}{4^{99}}\)
$4A=1+\frac{1}{4}+....+\frac{1}{4^{98}}$
$\Rightarrow 4A-A=(1+\frac{1}{4}+....+\frac{1}{4^{98}})-(\frac{1}{4}+\frac{1}{4^2}+...+\frac{1}{4^{99}})$
$\Rightarrow 3A=1-\frac{1}{4^{99}}< 1$
$\Rightarrow A< \frac{1}{3}$


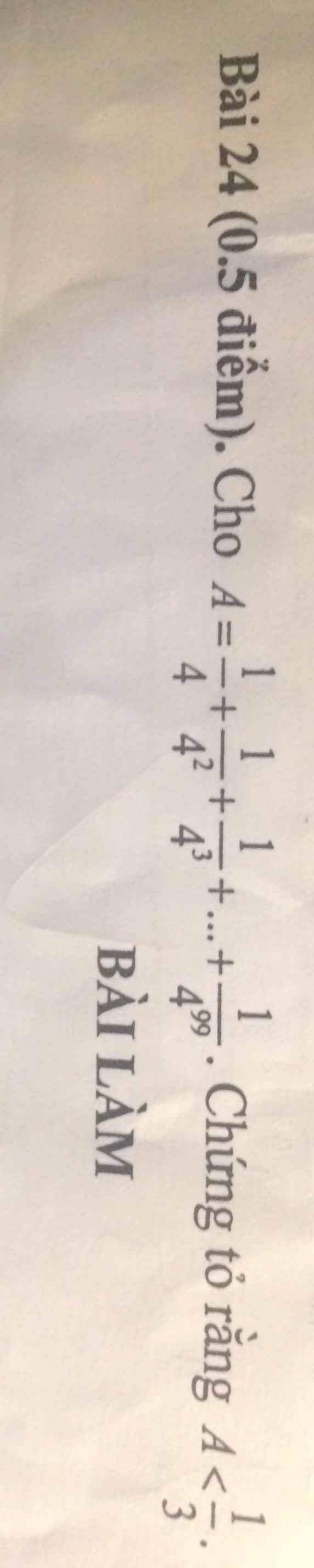





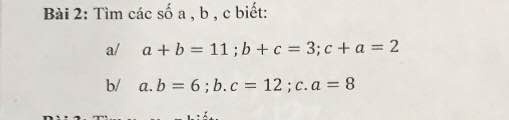

 làm câu 10,11,12 chỉ vẽ hình thôi nếu giải thì giải hộ ạ
làm câu 10,11,12 chỉ vẽ hình thôi nếu giải thì giải hộ ạ