a) \(M=\left(\dfrac{\sqrt{x}+2}{x-2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right).\dfrac{\left(\sqrt{x}-1\right)^2}{2\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)^2}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{\left(\sqrt{x}-1\right)^2}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{2\sqrt{x}}\)
\(=\dfrac{6\sqrt{x}}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{2\sqrt{x}}=\dfrac{3}{\sqrt{x}+1}\)
b) \(M\in Z\Rightarrow\dfrac{3}{\sqrt{x}+1}\in Z\Rightarrow3⋮\sqrt{x}+1\Rightarrow\sqrt{x}+1\in\left\{1;3\right\}\left(\sqrt{x}+1>0\right)\)
\(\Rightarrow x\in\left\{0;4\right\}\)

 giải giúp
giải giúp


 giải giúp
giải giúp giải giúp
giải giúp Giải giúp
Giải giúp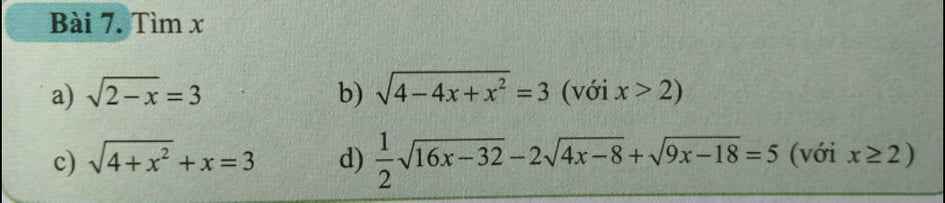 Giải giúp a b
Giải giúp a b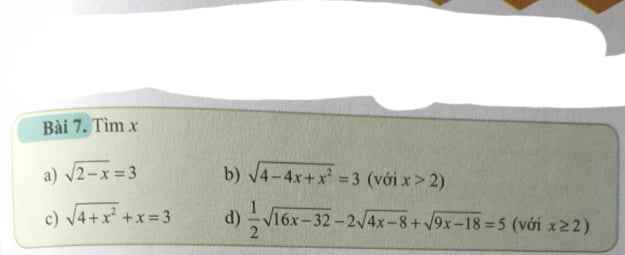 giải giúp c d
giải giúp c d giải giúp câu c
giải giúp câu c giải giúp a b
giải giúp a b

