a, \(A=\dfrac{\sqrt{x}-1+3}{\sqrt{x}-1}=1+\dfrac{3}{\sqrt{x}-1}\)
- Để biểu thức A nhận giá trị nguyên
\(\Leftrightarrow\sqrt{x}-1\inƯ_{\left(3\right)}\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{2;0;4;-2\right\}\)
\(\Leftrightarrow x\in\left\{0;4;16\right\}\)
Vậy ...
b, \(B=\dfrac{2\sqrt{x}+4-7}{\sqrt{x}+2}=2-\dfrac{7}{\sqrt{x}-1}\)
- Để biểu thức B nhận giá trị nguyên
\(\Leftrightarrow\sqrt{x}+2\inƯ_{\left(7\right)}\)
\(\Leftrightarrow\sqrt{x}+2\in\left\{1;-1;7;-7\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{-1;-3;5;-9\right\}\)
\(\Leftrightarrow x\in\left\{25\right\}\)
Vậy ...

 giải giúp
giải giúp





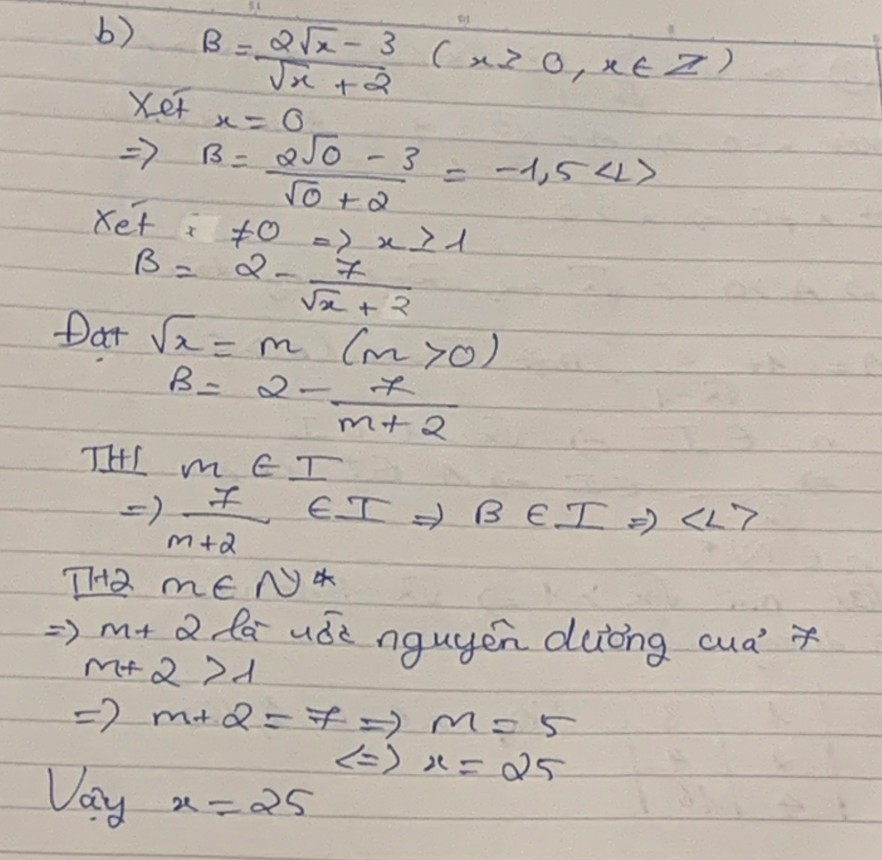
 giải giúp
giải giúp giải giúp
giải giúp Giải giúp
Giải giúp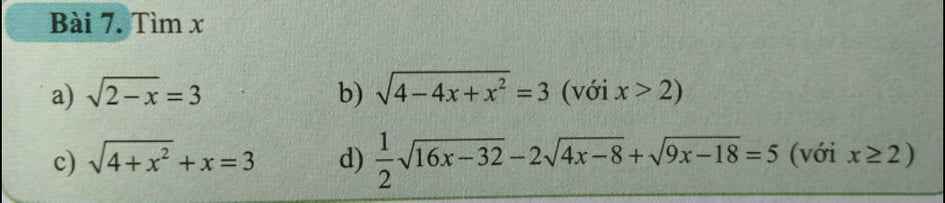 Giải giúp a b
Giải giúp a b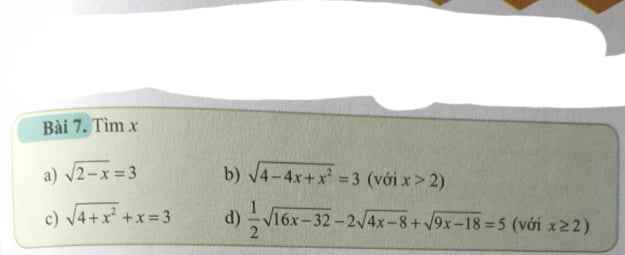 giải giúp c d
giải giúp c d giải giúp câu c
giải giúp câu c giải giúp a b
giải giúp a b

