giải giúp mình câu 6 ạ
Câu 6:
1: Ta có \(\Delta'=\left(m-1\right)^2-4\left(m-5\right)=m^2-6m+21=\left(m-3\right)^2+12>0\) nên phương trình đã cho luôn có 2 nghiệm phân biệt.
2: Theo hệ thức Viète ta có \(\left\{{}\begin{matrix}x_1x_2=m-5\\x_1+x_2=2\left(m-1\right)\end{matrix}\right.\).
Ta có \(10=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4\left(m-1\right)^2-2\left(m-5\right)\Leftrightarrow4m^2-10m+4=0\Leftrightarrow2\left(m-2\right)\left(2m-1\right)=0\Leftrightarrow\left[{}\begin{matrix}m=2\\m=\dfrac{1}{2}\end{matrix}\right.\).
Vậy...
Câu 5: \(\left\{{}\begin{matrix}4x-5y=-5\\4x-7y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-5y=-5\\2y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\x=\dfrac{-15}{4}\end{matrix}\right.\)
Mình nhầm đoạn Delta':
\(\Delta'=\left(m-1\right)^2-\left(m-5\right)=m^2-3m+6>0\)
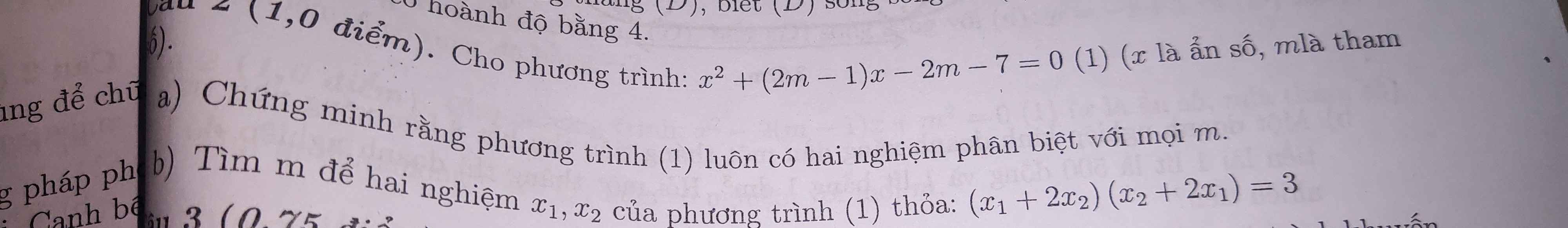
Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !