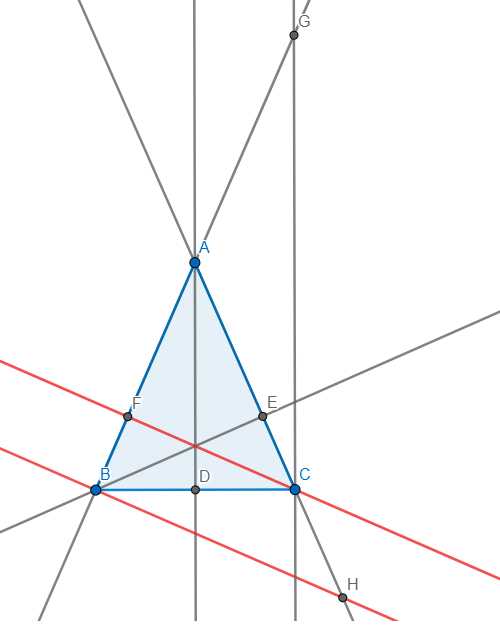
Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)