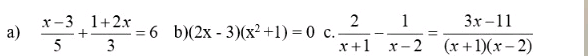a) \(\dfrac{x-3}{5}+\dfrac{1+2x}{3}=6\)
\(\Leftrightarrow\dfrac{3\left(x-3\right)}{15}+\dfrac{5\left(1+2x\right)}{15}=\dfrac{90}{15}\)
\(\Leftrightarrow3\left(x-3\right)+5\left(1+2x\right)=90\)
\(\Leftrightarrow3x-9+5+10x=90\)
\(\Leftrightarrow13x-4=90\)
\(\Leftrightarrow13x=90+4\)
\(\Leftrightarrow13x=94\)
\(\Leftrightarrow x=\dfrac{94}{13}\)
Vậy \(S=\left\{\dfrac{94}{13}\right\}\)
b) \(\left(2x-3\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x^2+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\left(tm\right)\\x^2=1\left(ktm\right)\end{matrix}\right.\)
Vậy \(S=\left\{1\right\}\)
c) \(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\)
\(\Leftrightarrow2\left(x-2\right)-\left(x+1\right)=3x-11\)
\(\Leftrightarrow2x-4-x-1=3x-11\)
\(\Leftrightarrow x-5=3x-11\)
\(\Leftrightarrow x-3x=5-11\)
\(\Leftrightarrow-2x=-6\)
\(\Leftrightarrow x=3\)
Vậy \(S=\left\{3\right\}\)