Question

Đoán nhận số nghiệm của các hệ phương trình sau đây bằng hình học:

a)  \(\left\{{}\begin{matrix}2x-y=1\\x-2y=-1\end{matrix}\right.;\)                       

b)  \(\left\{{}\begin{matrix}2x+y=4\\-x+y=1\end{matrix}\right..\)

Answer 1

a)

Vẽ (d₁): 2x - y = 1

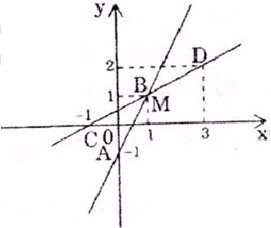
Cho x = 0 => y = -1, ta được A(0; -1).

Cho y = 0 => x = 1, được B(1; 1).

Vẽ (d₂): x - 2y = -1

Cho x = 1 => y = 0, được C (-1; 0)).

Cho y = 2 => x = 3, được D = (3; 2).

Hai đường thẳng cắt nhau tại điểm M có tọa độ (x = 1, y = 1).

Thay x = 1, y = 1 vào các phương trình của hệ ta được:

2 . 1 - 1 = 1 (thỏa mãn)

1 - 2 . 1 = -1 (thỏa mãn)

Vậy hệ phương trình có một nghiệm (x; y) = (1; 1).

b)

Vẽ (d₁): 2x + y = 4

Cho x = 0 => y = 4, được A(0; 4).

Cho y = 0 => x = 2, được B(2; 0).

Vẽ (d₂): -x + y = 1

Cho x = 0 => y = 1, được C(0; 1).

Cho y = 0 => x = -1, được D(-1; 0).

Hai đường thẳng cắt nhau tại điểm N có tọa độ (x = 1; y = 2).

Thay x = 1, y = 2 vào các phương trình của hệ ta được:

2 . 1 + 2 = 4 và -1 + 2 = 1 (thỏa mãn)

Vậy hệ phương trình có một nghiệm (x; y) = (1; 2).