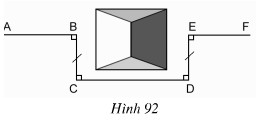
Bài giải:
Tứ giác BCDE có:
BC // DE (vì cùng vuông góc với CD)
BC = DE
nên BCDE là hình chữ nhật
Do đó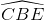 
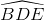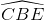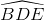= 900 , 
= 900
Suy ra AB và EF cùng nằm trên một đường thẳn
Đố: Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn như hình dưới. Đội đã dựng các điểm C, D, E như dưới hình vẽ rồi trồng cây trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng ?
Bài 5. Cho hình chữ nhật ABCD. Nối C với một điểm E bất kì trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại H và K. Chứng minh:
a) Tứ giác AHFK là hình chữ nhật
b) AF // BD;
c) Ba điểm E, H, K thẳng hàng.
Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (hình vẽ). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.
Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Lấy điểm M thuộc đoạn thẳng OC. Gọi E, F lần lượt là hình chiếu của điểm M trên đường thẳng AB, AD. Chứng minh:
a) Tứ giác AEMF là hình chữ nhật.
b) BD // EF.
+ vẽ hình nhé
Bài 4. (3,5 điểm) Cho tam giác ABC vuông tại A, đường cao AH, M là một điểm bất kì trên cạnh BC. Qua M kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và D. a) Tứ giác ADME là hình gì? Vì sao? b) Tính hat DHE c) Lấy điểm I đối xứng với M qua D, điểm K đối xứng với M qua E. Chứng minh I, A, K thẳng hàng. d) Xác định vị trí của điểm M để đoạn thẳng DE có độ dài nhỏ nhất?
ΔABC vuông tại A, đường cao AH. D,E là hình chiếu của H trên AB,AC
a, AH=DE
b, I,K lần lượt là trung điểm HB,HC. C/m DI//EK
c, O là giao điểm của AH, DE
M là giao điểm của DH,OI
N là giao điểm của CF,EF. C/m OMHN LÀ HCN
Các bạn ko cần vẽ hình đâu, giải giùm mik câu b,c thui. Mik đang cần gấp
Bài 3: Cho tam giác ABC vuông cân tại A, AC = 4cm, Điểm M thuộc cạnh BC.
Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC.
a. Tứ giác EDME là hình gì? tính chu vi tứ giác đó.
b. Điểm M ở vị trí nào trên cạnh BC thì đoạn thẳng DE có độ dài nhỏ nhất
Cho tam giác ABC cân tại A. Từ một điểm D trên đáy BC, vẽ đường thẳng vuông góc với BC cắt các đường thẳng AB, AC lần lượt tại N và M. gọi H và K lần lượt là trung điểm của BC và MN. Chứng minh rằng tứ giác AKDG là hình chữ nhật
cho tg ABC cân tại A. Từ điểm D trên BC kẻ đường vuông góc với BC cắt AB, Ac lần lượt tại E, F. Dựng các hình chữ nhật BDEH và CDFK
a) CM: Ba điểm A, H, K thẳng hàng
b) CM: A là trung điểm của HK
c) Gọi I, J theo thứ tự là tâm của các hình chữ nhật BDEH và CDFK. Tìm tập hợp trung điểm M của IJ khi D di động trên BC
