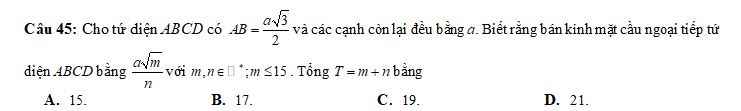Lời giải:
Áp dụng định lý pitago thì độ dài đường sinh của hình nón là:
\(l=\sqrt{r^2+h^2}=\sqrt{a^2+3a^2}=2a\)
Do đó diện tích xung quanh của hình nón là:
\(S_{xq}=\pi rl =\pi. a.2a=2\pi a^2\)
cắt một hình nón bằng một mặt phẳng đi qua trục của nó, ta được thiết diện là một tam giác đều cạnh \(2a\sqrt{2}\) . Diện tích xung quanh của khối nón là:
cho hình nón có bán kính đáy R, góc giữa đường sinh và đáy của hình nón là anpha. một mặt phẳng (P) sog song với đáy của hình nón, cách đáy hình nón một khoảng h, cắt hình nón theo đường tròn (C). tính bán kính đtron (C) theo R,h và anpha
Khối hộp ABCDA'B'C'D' có đáy là hình chữ nhật với AB=\(\sqrt{3}\) ; AD=\(\sqrt{7}\) . Các đường chéo AC' và DB' lần lượt tao với đáy các góc 45 hoặc 60, chiều cao của nó bằng 2, tính thể tích lăng trụ.
A.2B.4C.3D.1Trong không gian cho tam giác vuông OIM vuông tại I, góc OMI bằng 60 độ và cạnh IM bằng 2a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay có diện tích xung quanh là:
Trong không gian cho tam giác vuông OIM vuông tại I, góc OMI bằng 60 độ và cạnh IM bằng 2a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay có diện tích xung quanh là:
HELP ME!!!!!
1> Cho hình chóp S.ABC có đáy là tam giác cân, AB = AC = a, (SBC) vuông góc với (ABC) và SA = SB =a. Cmr ∆ SBC vuông. Biết SC= x, tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC
2> Cho lăng trụ đứng tam giác ABC.A’B’C’ biết AA’ = AB = a, AC = 2a và góc BAC = 60⁰. Gọi M = A’C ∩ AC’. Tính thể tích tứ diện MBB’C và tính bán kính mặt cầu ngoại tiếp hình lăng trụ.
Trong không gian cho hình chữ nhật ABCD có AB=1, AD=2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó.
Trong không gian cho hình chữ nhật ABCD có AB=1, AD=2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó.
Cho tứ diện ABCD có \(AB=\dfrac{a\sqrt{3}}{2}\) và các cạnh còn lại đều bằng \(a\) . Biết rằng bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng \(\dfrac{a\sqrt{m}}{n}\) với \(m,n\in N\)*; \(m\le15\). Tổng \(T=m+n\) bằng?
A. 15 B. 17 C. 19 D. 21
Có gì cho mình xin công thức chung để tính bán kính mặt cầu ngoại tiếp tứ diện luôn ạ, mình cảm ơn nhiều♥
