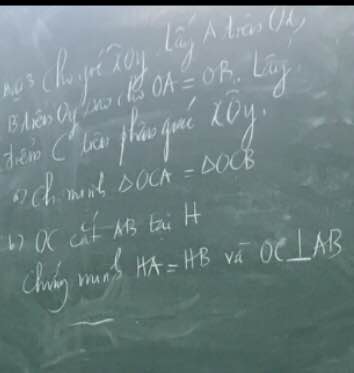Bài 2:
a: Xét ΔABD vuông tại D và ΔACD vuông tại D có
AB=AC
AD chung
Do đó: ΔABD=ΔACD
b: Xét ΔAEK và ΔAFK có
AE=AF
\(\widehat{EAK}=\widehat{FAK}\)
AK chung
Do đó: ΔAEK=ΔAFK
Suy ra: \(\widehat{AEK}=\widehat{AFK}=90^0\)
hay KF⊥AC
c: Xét ΔEBC vuông tại E và ΔFCB vuông tại F có
BC chung
\(\widehat{EBC}=\widehat{FCB}\)
Do đó:ΔEBC=ΔFCB
Suy ra: \(\widehat{KBC}=\widehat{KCB}\)
hayΔKBC cân tại K
d: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
Đúng 1
Bình luận (0)
