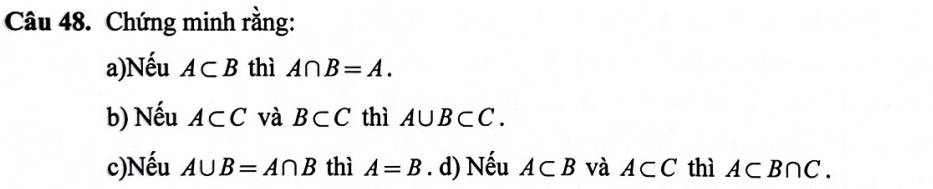Chương 1: MỆNH ĐỀ, TẬP HỢP
Các câu hỏi tương tự
mình đc gợi ý là giải bằng cách sơ đồ ven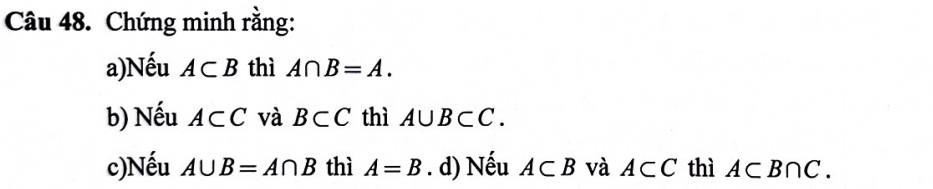
Chứng minh theo quy nạp
Dãy số Fn=2^2^n +1 với n thuộc N gọi là các số Fermat
a) Chứng minh Fn=F0F1....Fn-1 +2 với mọi n nguyên dương
b) Từ đó chứng minh (Fm,Fn)=1 với mọi m khác n nguyên dương
1. Cho n là 1 số tự nhiên. hỏi có bao nhiêu số tự nhiên không vượt quá n và chia hết cho 1 số tự nhiên k nào đó
2.Cho A là tập hợp con thực sự khác rỗng của tập hợp số nguyên Z thỏa mãn tính chất :
i) forall a,bin A thì left{{}begin{matrix}-ain Aa+bin Aend{matrix}right. ii) 5in A
Cmr: mọi phần tử của A đều chia hết cho 5
3. Chứng minh quy tắc De morgan thì làm cách nào ạ?
4. Chứng minh nguyên lí bao hàm và loại trừ cho 3 tập hợp A,B,C thì vẽ sơ đồ Venn hay làm như thế nào?
@A...
Đọc tiếp
1. Cho n là 1 số tự nhiên. hỏi có bao nhiêu số tự nhiên không vượt quá n và chia hết cho 1 số tự nhiên k nào đó
2.Cho A là tập hợp con thực sự khác rỗng của tập hợp số nguyên Z thỏa mãn tính chất :
i) \(\forall a,b\in A\) thì \(\left\{{}\begin{matrix}-a\in A\\a+b\in A\end{matrix}\right.\) ii) \(5\in A\)
Cmr: mọi phần tử của A đều chia hết cho 5
3. Chứng minh quy tắc De morgan thì làm cách nào ạ?
4. Chứng minh nguyên lí bao hàm và loại trừ cho 3 tập hợp A,B,C thì vẽ sơ đồ Venn hay làm như thế nào?
@Akai Haruma, @Nguyễn Việt Lâm
Giúp em với ạ! Em cảm ơn nhiều
Cho tam giác ABC, có hai đường trung tuyến BM, CN. Chứng minh tam giác ANC = tam giác AMB. Chứng minh CN = BM
a) Cho tam giác ABC. Chứng minh rằng:.b) Cho tam giác , trên lấy điểm sao cho . Gọi là điểm thoả mãn hệ thức: . Chứng minh ba điểm , , thẳng hàng.
chứng minh bất đẳng thức
Cho u \(\le\) v . Chứng minh rằng u3 - 3u \(\le\)v3 - 3v + 4
chứng minh phản chứng mệnh đề : "pt 15x^2 - 7y^2 = 9 không có nghiệm nguyên"
Dùng phương pháp chứng minh phản chứng, chứng minh định lý sau: "Với mọi số nguyên dương a,b nếu a2+b2 chia hết cho 8 thì a,b không đồng thời là các số lẻ"
Dùng phản chứng hoặc qui nạp, chứng minh rằng: 2008^2012 + 2009^2012 < 2010^2012