Chứng minh tam giác vuông:
Ứng dụng:
- Vẽ đường tròn (A, r) với r = AB/2; vẽ đường tròn (B, r).
- Gọi C là giao điểm của hai cung tròn nằm ở phía trong tờ giấy.
- Trên tia BC lấy D sao cho BC = CD => AB ⊥ AD.
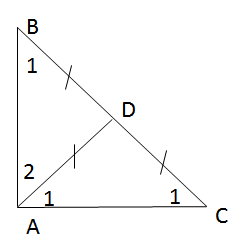
Thật vậy: ΔABD có AC là trung tuyến ứng với BD (BC = CD) và AC = BC = CD.
=> AC = BD => ∆ABD vuông tại A.
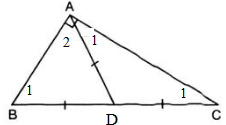
Giả sử ∆ABC có AD là đường trung tuyến ứng với BC và DA=12BC=>AD=BD=DCDA=12BC=>AD=BD=DC
Hay ∆ADC, ∆ADB cân tại D. Do đó:
ˆA1=ˆC1ˆA2=ˆB1}=>ˆA1+ˆA2=ˆB1+ˆC1A1^=C1^A2^=B1^}=>A1^+A2^=B1^+C1^
Mà ˆA1+ˆA2+ˆB1+ˆC1=1800A1^+A2^+B1^+C1^=1800 (tổng các góc ∆ABC)
=> ˆA1+ˆA2=900A1^+A2^=900 Hay ∆ABC vuông tại A.
Áp dụng
-Vẽ đường tròn (A;r); r=AB2r=AB2; vẽ đường tròn (B, r)
-Gọi C là giao điểm của 2 cung tròn nằm ở phía trong tờ giấy.
-Trên tia BC lấy D sao cho BC = CD => AB ⊥ AD.
Thật vậy: ∆ABD có AC là trung tuyến ứng với BD (BD = CD) và AC = BC = CD.
=> \(AC = {1 \over 2}BD
=> ∆ ABD vuông tại A