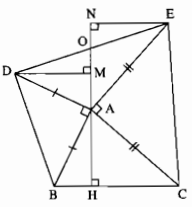
a) Ta có :
góc HAB + góc BAD + góc DAM = 180 độ (kề bù)
=> góc HAB + 90 độ + góc DAM = 180 độ
=> góc HAB + góc DAM = 90 độ
=> góc HAB = 90 độ - góc DAM (1)
Xét tam giác AMD : góc AMD = 90 độ
=> góc DAM + góc ADM = 90 độ
=> góc ADM = 90 độ - góc DAM
Từ (1) và (2) => góc HAB = góc ADM
Xét tam giác ADM và tam giác BAH :
góc AMD = góc BHA (= 90∘)
AD = AB (gt)
góc ADM = BAH (cmt)
==> ∆ADM = ∆BAH (cạnh huyền - góc nhọn)
=> DM = AH (2 cạnh tương ứng)
b) Ta có:
góc HAC + góc CAE + góc EAN = 180 độ (kề bù)
=> góc HAC + 90 độ + góc EAN = 180 độ
=> góc HAC + góc EAN = 90 độ
=> góc EAN = 90 độ - góc HAC (3)
Xét tam giác AHC : góc AHC = 90 độ
=> góc HAC + góc HCA = 90 độ
=> góc HCA = 90 độ - góc HAC (4)
Từ (3) và (4) => góc HCA = góc EAN
Xét tam giác AHC và tam giác ENA :
góc AHC = góc ENA (= 90 độ)
AC = EA (gt)
góc HCA= góc NAE (cmt)
==> ∆AHC = ∆ENA (cạnh huyền - góc nhọn)
=> AH = EN (2 cạnh tương ứng)
mà DM = AH (chứng minh ở câu a)
==> EN = DM (= AH)
DM⊥AH ; EN⊥AH
=> DM // EN
=> góc MDO = góc NEO (so le trong)
Gọi O là giao điểm MN và DE
Xét tam giác DMO và tam giác ENO :
góc DMO = góc ENO (=90 độ)
DM = EN (cmt)
góc MDO = góc NEO (cmt)
==> ∆DMO = ∆ENO (g.c.g)
=> OD = DE (2 cạnh tương ứng)
Vậy MN đi qua trung điểm của DE
(- Bài này t học rồi, đảm bảo chi tiết và đúng :)) t lấy vở của t ra chép lại cho bn đấy =))













