Chương 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
Các câu hỏi tương tự
Cho tứ giác ABCD nội tiếp (O;R). AC vuông góc với BD và AC cắt BD tại I. Gọi trung điểm của AB là M. Chứng minh rằng MI vuông góc với DC
cho tứ giác ABCD . Gọi M , N lần luợt là trung điểm của AC và BD . Chứng minh rằng : AB2 + BC2 + CD2 +DA2 = AC2 + BD2 + 4MN2
Cho tam giác ABC không cân. Đường tròn tâm I nội tiếp tam giác , tiếp xúc với các cạnh BC, CA, AB lần lượt tại A', B', C' . Đường thằng B'C' cắt BC tại D. Chứng minh ID vuông góc với AA'
Cho hình thang ABCD có \(\overrightarrow{2AB}=\overrightarrow{DC}\),AC=8,BD=6,góc tạo bởi 2 vecto \(\overrightarrow{AC}\) và \(\overrightarrow{BD}\) bằng 120.Tính độ dài các cạnh AD,BC
Cho tam giác abc có bc=a;ac=b;ab=c ;I là tâm đường tròn nội cmt aIA^2+b×IB^2+c
Cho tam giác ABC có AB=3, AC=7, BC=8.
a) tính diện tích tam giác ABC.
b) Tính bán kính đường tròn nội tiếp, ngoại tiếp của tam giác.
c) Tính đường cao kẻ từ đỉnh A.
1. Cho tam giác ABC vuông tại A, AB = 5, AC = 7. Tính giá trị của \(\overrightarrow{AB}\).\(\overrightarrow{BC}\)?
2. Cho hình chữ nhật ABCD, AB = 8, AD = 5. Tính giá trị của \(\overrightarrow{AB}\).\(\overrightarrow{BD}\)?
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức (1.0 điểm). Chứng minh đẳng thức .
Đọc tiếp
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức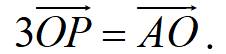
(1.0 điểm). Chứng minh đẳng thức .
cho hình vuông ABCD cạnh a . G ọi N là trung điểm của CD , M là điểm trên AC sao cho AM = \(\frac{1}{4}\) AC : a) tính các cạnh của tam giác BMN ; b) có nhận xét gì về tam giác BMN ? tính diện tích tam giác đó ; c) gọi I là giao điểm của BN và AC , tính CI ; d) tính bán kính đường tròn ngoại tiếp tam giác BDN










