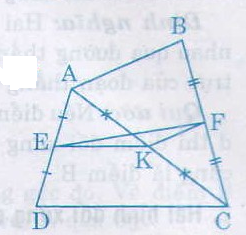
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2 = (AB+CD)/2
Vậy EF ≤ (AB+CD)/2
27. Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng EF \(\le\dfrac{AB+CD}{2}\)
Bài giải:

a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK =\(\dfrac{CD}{2}\)
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = \(\dfrac{AB}{2}\)
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = \(\dfrac{CD}{2}\) + \(\dfrac{AB}{2}\) = \(\dfrac{\left(AB+CD\right)}{2}\)
Vậy EF ≤ \(\dfrac{\left(AB+CD\right)}{2}\)










