Question

Cho tứ diện ABCD, gọi M là trung điểm của AC, trên cạnh AD lấy điểm N sao cho AN = 2ND,  trên cạnh BC lấy điểm Q sao cho BC = 4.PQ. Gọi I là giao điểm của đường thẳng MN và mặt phẳng (BCD), J là giao điểm của đường thẳng BD và mặt phẳng (MNQ). Khi đó JB/ JD + JQ/JI bằng 

Answer 1

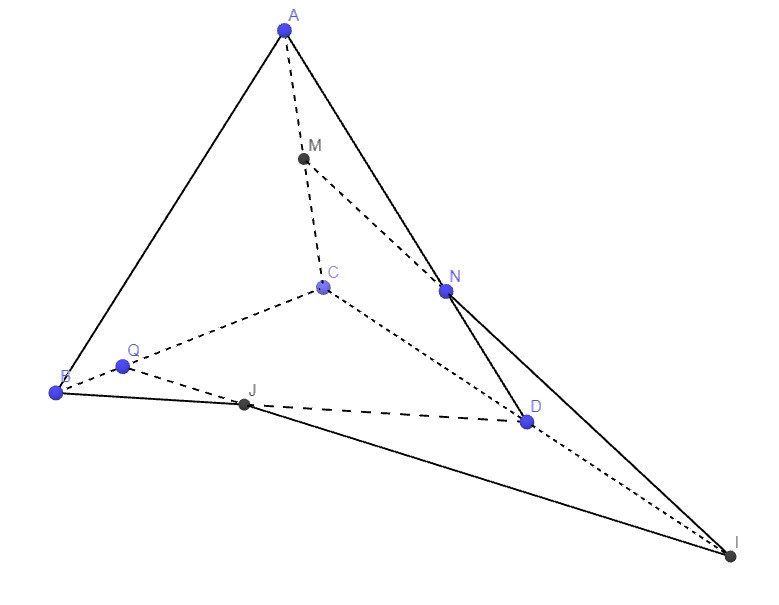
Trong mp (ACD) kéo dài MN và CD cắt nhau tại I

Trong mp (BCD) nối IQ cắt BD tại J

Áp dụng định lý Menelaus trong tam giác ACD:

\(\dfrac{AM}{MC}.\dfrac{CI}{ID}.\dfrac{DN}{NA}=1\Rightarrow1.\dfrac{CI}{ID}.\dfrac{1}{2}=1\Rightarrow IC=2ID\)

Do \(BC=4BQ\Rightarrow QC+QB=4QB\Rightarrow QC=3QB\)

Menelaus cho tam giác BCD:

\(\dfrac{QC}{QB}.\dfrac{BJ}{JD}.\dfrac{DI}{IC}=1\Rightarrow3.\dfrac{BJ}{JD}.\dfrac{1}{2}=1\Rightarrow\dfrac{BJ}{JD}=\dfrac{2}{3}\)

Menelaus cho tam giác CQI:

\(\dfrac{ID}{DC}.\dfrac{CB}{BQ}.\dfrac{QJ}{JI}=1\Rightarrow1.4.\dfrac{JQ}{JI}=1\Rightarrow\dfrac{JQ}{JI}=\dfrac{1}{4}\)

\(\Rightarrow\dfrac{JB}{JD}+\dfrac{JQ}{JI}=\dfrac{2}{3}+\dfrac{1}{4}=\dfrac{11}{12}\)

Answer 2

Điểm P là điểm nào em nhỉ?

Answer 3