Question

Cho tam giác vuông ABC ( \(\widehat{A}\) vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A'. Chứng minh rằng:

a) BA và BA' là hai tiếp tuyến cắt nhau của (C; CA).

b) CA và CA' là hai tiếp tuyến cắt nhau của (B; BA).

Answer 1

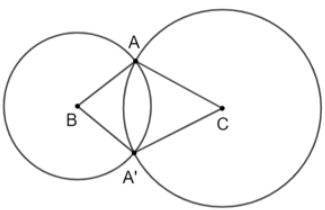
a) Xét tam giác ABC và tam giác A’BC có:

BA = BA’

BC chung

CA = CA’

Suy ra: \(\Delta {\rm{ABC}} = \Delta {\rm{A'BC}}\)(c.c.c)

Do đó: \(\widehat {{\rm{BA'C}}} = \widehat {{\rm{BAC}}} = 90^\circ \) (hai góc tương ứng)

Suy ra: \({\rm{CA'}} \bot {\rm{BA'}}\) tại A’ nên BA’ là tiếp tuyến của (C; CA)

Lại có: \({\rm{CA}} \bot {\rm{BA}}\) tại A nên BA là tiếp tuyến của (C; CA)

Vậy BA và BA’ là hai tiếp tuyến cắt nhau của (B; BA).

b) \({\rm{CA'}} \bot {\rm{BA'}}\) tại A’ nên CA’ là tiếp tuyến của (B; BA)

\({\rm{CA}} \bot {\rm{BA}}\) tại A nên CA là tiếp tuyến của (B; BA)

Vậy CA và CA’ là hai tiếp tuyến cắt nhau của (C; CA).