Question

Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung \(\overset\frown{BD};\overset\frown{BE};\overset\frown{EC}\).

Answer 1

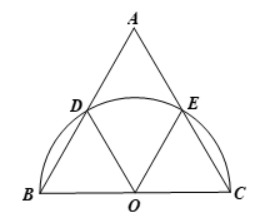
Gọi O là tâm đường tròn đường kính BC.

Ta có OB = OD (= R)

Vậy tam giác BOD cân tại O

Mà \(\widehat {DBO}\)= 60^o nên tam giác BOD đều

Suy ra \(\widehat {DOB}\)= 60^o

OE = DC (= R)

Vậy tam giác EOC cân tại O

Mà \(\widehat {ECO}\)= 60^o nên tam giác EOC đều

Suy ra \(\widehat {EOC}\)= 60^o

Ta có \(\widehat {BOD} + \widehat {DOE} + \widehat {EOC} = {180^o}\)

Suy ra 60^o + \(\widehat {DOE} + {60^o} = {180^o}\) nên \(\widehat {DOE} = {60^o}\)

Vì \(\widehat {BOD} = \widehat {DOE} = \widehat {EOC} = {60^o}\) nên sđ\(\overset\frown{BD}\) = sđ\(\overset\frown{BE}\) = sđ\(\overset\frown{EC}={{60}^{o}}\)

Vậy \(\overset\frown{BD}=\overset\frown{BE}=\overset\frown{EC}\)