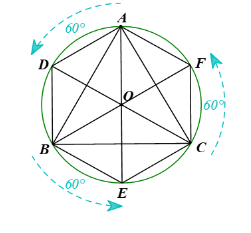
Vì lục giác ADBECF nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE = OF\).
Vì phép quay ngược chiều \({60^o}\) tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F nên \(\widehat {AOD} = \widehat {BOE} = \widehat {COF} = {60^o}\).
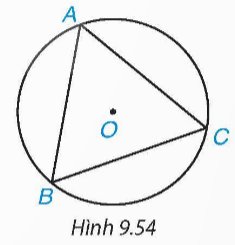
Vì tam giác ABC đều nên AO, BO là các đường phân giác của tam giác ABC.
Ta có: \(\widehat {BAO} = \widehat {ABO} = \frac{1}{2}\widehat {ABC} = {30^o}\)
Tam giác OAB có: \(\widehat {BOA} = {180^o} - \widehat {BAO} - \widehat {ABO} = {120^0}\).
Suy ra: \(\widehat {BOD} = \widehat {AOB} - \widehat {AOD} = {60^o}\)
Tam giác AOD cân tại O (do \(OA = OD\)), mà \(\widehat {AOD} = {60^o}\) nên tam giác DAO đều.
Do đó, \(DA = AO = OD,\widehat {DAO} = \widehat {ADO} = {60^o}\)
Tương tự ta có: \(DO = OB = BD,\widehat {ODB} = \widehat {OBD} = {60^o}\), \(EO = OB = BE,\widehat {OEB} = \widehat {OBE} = {60^o}\), \(EO = OC = CE,\widehat {OEC} = \widehat {OCE} = {60^o}\), \(FO = OC = CF,\widehat {OFC} = \widehat {OCF} = {60^o}\), \(FO = OA = AF,\widehat {OFA} = \widehat {OAF} = {60^o}\)
Do đó, \(AD = BD = BE = EC = FC = FA\) và \(\widehat {DAF} = \widehat {AFC} = \widehat {FCE} = \widehat {CEB} = \widehat {EBD} = \widehat {BDA} = {120^o}\)
Vậy ADBECF là lục giác đều.