Question

Cho tam giác BC. Từ một điểm M bất kì trong tam giác kẻ MD, ME, MF lần lượt vuông góc với các cạnh BC, CA, AB (h.8).

Chứng minh rằng :

                  \(BD^2+CE^2+AF^2=DC^2+EA^2+FB^2\)

Answer 1

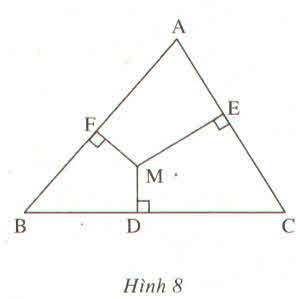
△DMC vuông tại D => DC²= MC² - MD²
△AME vuông tại E => EA² = AM² - ME²
△BMF vuông tại F => BF² = BM² - MF²
Suy ra DC² + EA² + BF² = MC² - MD² + AM² - ME² + BM² - MF² (1)
△BDM vuông tại D => BD^2 = BM^2 - MD^2
△CME vuông tại E => CE^2 = MC^2 - ME^2
△AMF vuông tại F => AF^2 = AM^2 - MF^2
Suy ra BD² + CE² + AF² = BM² - MD² + MC² - ME² + AM² - MF² (2)
Từ (1) và (2) => BD² + CE² + AF² = DC² + EA² + FB²