a) Xét \(\Delta AOD \) và \(\Delta BOD \) có:
\(\widehat{O_1}=\widehat{O_2}\) (gt)
OD là cạnh chung
OA = OB (gt)
Vậy \(\Delta AOD = \Delta BOD\) (c.g.c)
=> DA = DB (2 cạnh tương ứng)
b) Vì \(\Delta AOD = \Delta BOD\) nên \(\widehat{ADO}=\widehat{BDO}\) (2 góc tương ứng) (1)
Ta có: \(\widehat{AOD}\) kề bù với \(\widehat{BOD}\) nên \(\widehat{AOD}+\widehat{BOD}=180^0\) (2)
Từ (1) và (2) suy ra: \(\widehat{AOD}=\widehat{BOD}=\dfrac{180^0}{2}=90^0\)
=> OD \(\perp\) AB tại D.
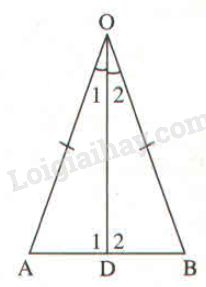
a) Xét ΔAOD∆AOD và ΔBOD∆BOD, ta có:
OA=OBOA=OB (gt)
ˆAOD=ˆBODAOD^=BOD^ (vì ODOD là tia phân giác góc OO)
ODOD cạnh chung
⇒ΔAOD=ΔBOD⇒∆AOD=∆BOD (c.g.c)
⇒DA=DB⇒DA=DB (hai cạnh tương ứng)
b) ΔAOD=ΔBOD∆AOD=∆BOD (chứng minh trên)
⇒ˆD1=ˆD2⇒D1^=D2^ (hai góc tương ứng)
Ta có: ˆD1+ˆD2=180∘D1^+D2^=180∘ (hai góc kề bù)
⇒ˆD1=ˆD2=90∘⇒D1^=D2^=90∘
Vậy OD⊥ABOD⊥AB.
Về hình vẽ: đã vẽ rồi nhưng ko bik sao để đăng nên mik chỉ đăng bài làm thôi nha!
a). C/m DA=DB?
Xét ΔAOD và ΔBOD có:
OD: cạnh chung (gt).
Góc O1= góc O2 (OD là tia p/g góc O)
OA=OB (gt).
⇒DA=DB nên ΔAOD=ΔBOD.
b). C/m OD⊥AB:
ΔAOD=ΔBOD nên góc D1 = góc D2 (2 góc tương ứng).
Ta có: góc D1+ góc D2= 180 độ.
Vì D là tia p/g nên 180/2= 90 độ.
Nên: góc D1= góc D2 = 90 độ.
⇒OD⊥AB.















