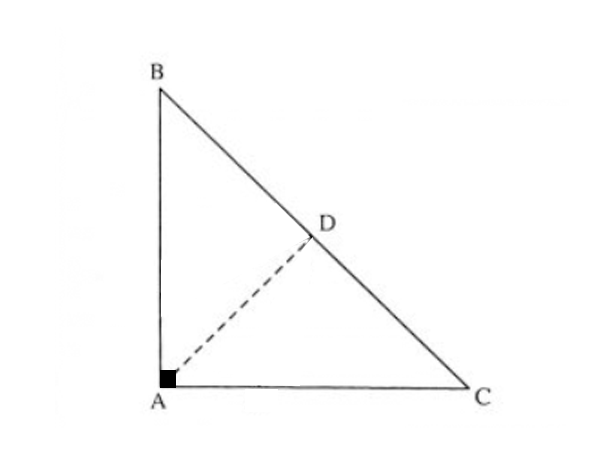
a) Cách 1:
Ta có \(\Delta ABC\) vuông tại \(A\left(gt\right)\) (1).
Mà \(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A (2).
Từ (1) và (2) => \(\Delta ABC\) vuông cân tại A.
=> \(\widehat{ABC}=\widehat{ACB}=45^0\) (tính chất tam giác vuông cân).
Cách 2:
Xét 2 \(\Delta\) \(ABD\) và \(ACD\) có:
\(AB=AC\left(gt\right)\)
\(BD=CD\) (vì D là trung điểm của \(BC\))
Cạnh AD chung
=> \(\Delta ABD=\Delta ACD\left(c-c-c\right)\)
=> \(\widehat{ABD}=\widehat{ACD}\) (2 góc tương ứng).
Hay \(\widehat{ABC}=\widehat{ACB}.\)
Xét \(\Delta ABC\) có:
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(90^0+\widehat{ABC}+\widehat{ACB}=180^0\)
=> \(\widehat{ABC}+\widehat{ACB}=180^0-90^0\)
=> \(\widehat{ABC}+\widehat{ACB}=90^0.\)
Mà \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
=> \(2.\widehat{ABC}=90^0\)
=> \(\widehat{ABC}=90^0:2\)
=> \(\widehat{ABC}=45^0.\)
b) Theo câu a) ta có \(\Delta ABD=\Delta ACD.\)
=> \(\widehat{ADB}=\widehat{ADC}\) (2 góc tương ứng).
Ta có: \(\widehat{ADB}+\widehat{ADC}=180^0\) (vì 2 góc kề bù).
Mà \(\widehat{ADB}=\widehat{ADC}\left(cmt\right)\)
=> \(2.\widehat{ADB}=180^0\)
=> \(\widehat{ADB}=180^0:2\)
=> \(\widehat{ADB}=90^0.\)
=> \(\widehat{ADB}=\widehat{ADC}=90^0\)
=> \(AD\perp BC\left(đpcm\right).\)
Chúc bạn học tốt!













