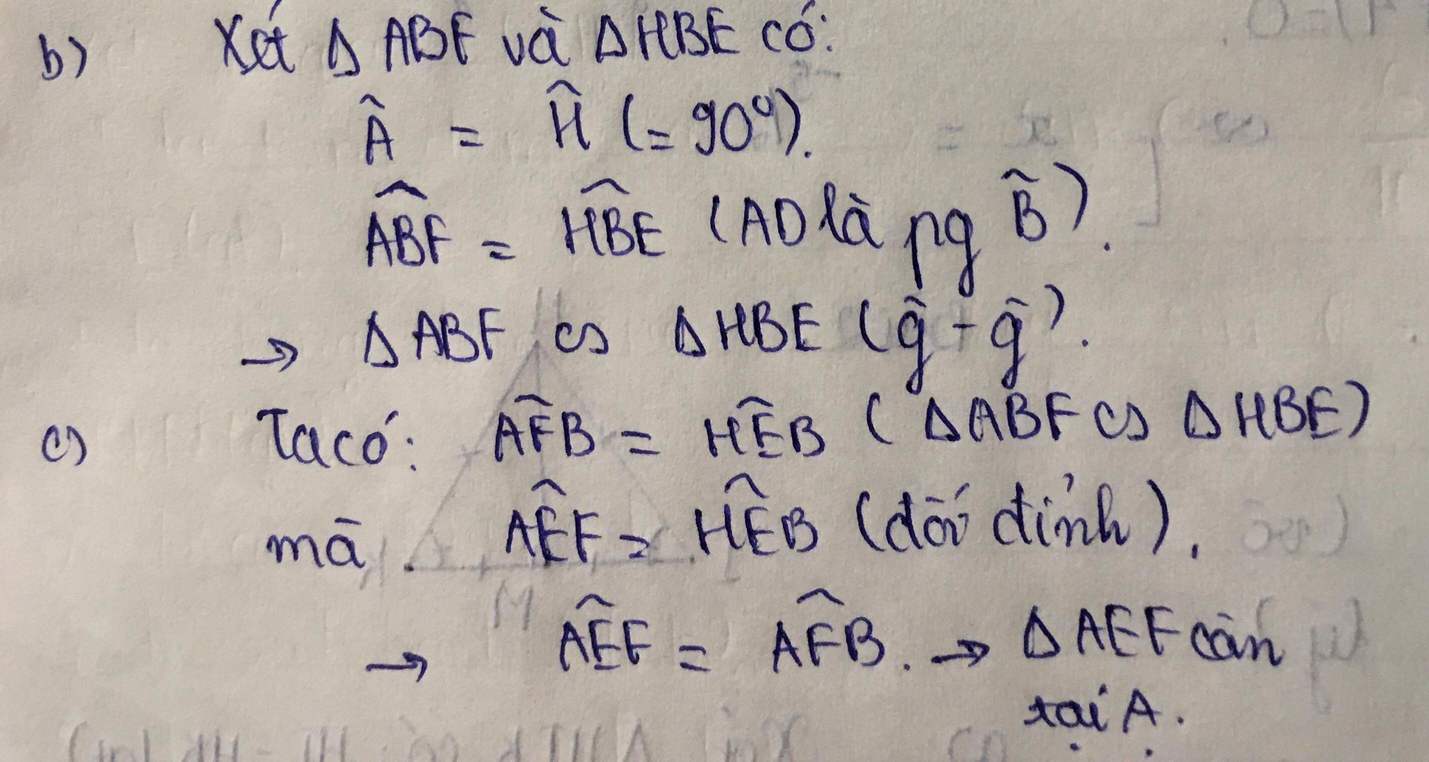Tam giác đồng dạng
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm, đường cao AH, tia phân giác của góc ABC cắt AC tại F và AH tại E. a) Tính BC, AF, FC b) Chứng minh tam giác ABC đồng dạng tam giác HBA c) Chứng minh AE.AF=EH.FC Mong các bạn ra đáp án giúp mình câu này với Thank you các bạn❤❤❤
cho tam giác ABC vuông tại A , AB=12cm , AC=16cm. Vẽ đường cao AH( H thuộc BC ) và tia phân giác của góc A cắt BC tại D a/ chứng minh tam giác HBA đồng dangj tam giác ABC b/ Tính độ dài cạnh BC c/ tính tỉ số diện tích của hai tam giác ABD và ACD d/ Tính độ dài các đoạn thẳng BD và CD
Cho tam giác ABC có Â = 90°, AB = 3cm và AC = 4 cm . Đường cao AH (H thuộc BC) a, chứng minh tam giác ABC đồng dạng tam giác HAC b, chứng minh AC² = BC.HC c,Tia phân giác góc A cắt BC tại D. Tính độ dài các đoạn thẳng BC , DB
Cho tam giác ABC vuông tại A. AB=3cm; AC=4cm. Vẽ AH.
a) chứng minh tam giác HBA đồng dạng tam giác ABC.
b) tính BC, AH, BH.
c) tia phân giác của góc B cắt AC và Ah theo thứ tự M và N. Kẻ IH song song với BN (I thuộc AC). Chứng minh AN2=NI.NC.
Help meeee câu c) với
cho tam giác abc vuông tại a (abac).vẽ ah vuông góc với bc tại h.a/chứng minh tam giác HAC đồng dạng tam giác ABCb/giả sử AB15cm,AC20cm.tính độ dài các cạnh AHc/vẽ tia phân giác của góc BAH cắt cạnh BH tại D.chứng minh BD/HDBC/AC.giải giúp mình với ạ. cho tam giác abc vuông tại a (abac).vẽ ah vuông góc với bc tại h.a/chứng minh tam giác HAC đồng dạng tam giác ABCb/giả sử AB15cm,AC20cm.tính độ dài các cạnh AHc/vẽ tia phân giác của góc BAH cắt cạnh BH tại D.chứng minh BD/HD...
Đọc tiếp
cho tam giác abc vuông tại a (ab<ac).vẽ ah vuông góc với bc tại h.
a/chứng minh tam giác HAC đồng dạng tam giác ABC
b/giả sử AB=15cm,AC=20cm.tính độ dài các cạnh AH
c/vẽ tia phân giác của góc BAH cắt cạnh BH tại D.chứng minh BD/HD=BC/AC.
giải giúp mình với ạ.
a/chứng minh tam giác HAC đồng dạng tam giác ABC
b/giả sử AB=15cm,AC=20cm.tính độ dài các cạnh AH
c/vẽ tia phân giác của góc BAH cắt cạnh BH tại D.chứng minh BD/HD=BC/AC.
giải giúp mình với ạ.
Cho tam giác ABC vuông tại A có AB = 20cm, AC = 21cm, đường phân giác của góc A cắt BC tại điểm D.
Tính BC, DB, DC (làm tròn đến phần trăm)
Gọi E, F lần lượt là hình chiếu của D lên AB, AC. Chứng minh ∆BED đồng dạng ∆BAC và tính tỉ số đồng dạng của chúng.
Tính diện tích tứ giác AEDF.
Cho ΔABC vuông tại A, có cạnh AB=3cm cạnh AC=4cm, AH là đường cao
a, chứng minh: ΔABC đồng dạng với ΔHBA
b,chứng minh: AB2 = BH.BC; AH2 = HB.HC
c, đường phân giác góc ABC cắt AH tại E và AC tại D, tính \(\dfrac{Sabc}{Shbe}\)
cho tam giác vuông abc vuông tại a biết ab = 6cm ac = 8cm đường cao AH a) chứng minh tam giác ABC tương đương tam giác HBA
b) chứng minh AB bình = AH.BC
c) tính AH
d) tia phân giác A cắt BC tại M, tính BM và MC
Cho tam giác ABC có ba góc nhọn . Đường cao AF , BE cắt nhau tại H . Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By vuông góc với BC . Tia Ax và By cắt nhau tại K .
a) Chứng minh : tam giác HAE đồng dạng với tam giác HBF.
b) Chứng minh : CE.CA=CF.CB.
c) Chứng minh góc CFE bằng góc CAB.
d) Nếu tam gics ABC cân tại C, chứng minh rằng ba điểm C, H, K thẳng hàng,