Ôn tập: Tam giác đồng dạng
Các câu hỏi tương tự
Cho tam giác ABC một đường thẳng song song với cạnh BC cắt AB tại D và AC tại E. Trên tia đối của tia CA lấy điểm F sao cho CF=BD. Gọi M là giao điểm của DF và BC Chứng minh rằng: MD/MF = AC/AB. Cho BC=8cm, BD=5cm, DE=3cm . Chứng minh tam giác ABC cân
Mik đang cần gấp!!!
Cho hình vuông ABCD có AB = a, hai đường chéo cắt nhau tại O. Trên hai cạnh AB, BC lần lượt lấy hai điểm E và G sao cho AE= BG. Gọi H là giao điểm của tia AG và tia DC, I là giao điểm của tia OG và đoạn thẳng BH.
1) Chứng minh rằng: AOGE là tam giác vuông cân.
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.
Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại P. Biết rằng AP = 2PK và CP = 2PM.
Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC ?
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.a) Chứng minh rằng : widehat{DMI}widehat{AME}b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!
Đọc tiếp
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.
a) Chứng minh rằng : \(\widehat{DMI}=\widehat{AME}\)
b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!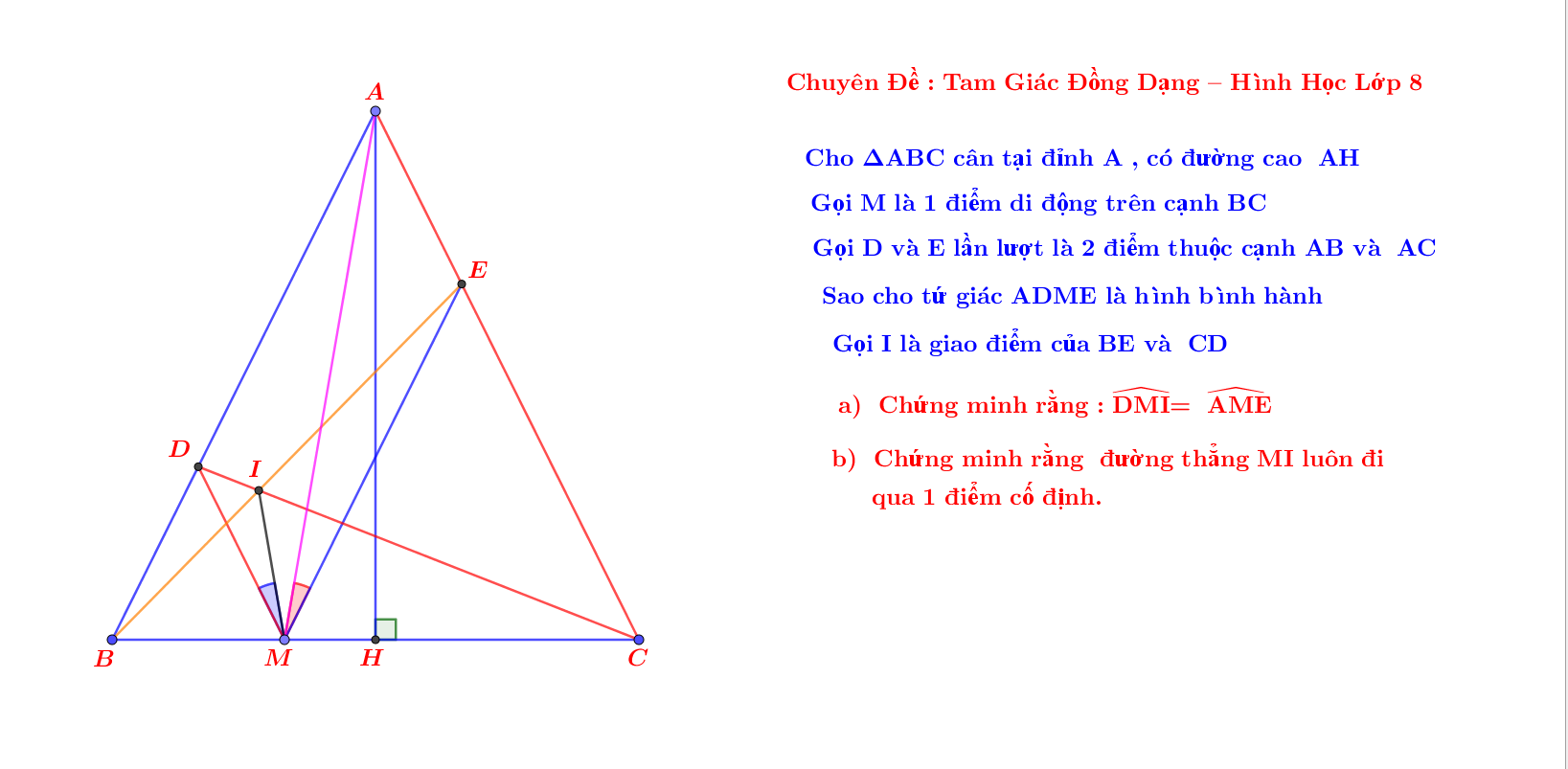
Bài 3: Cho tam giác ABC vuông tại A (AC>AB), M là điểm trên cạnh AC. Vẽ MD vuông góc với BC tại D. Gọi E là giao điểm của hai đường thẳng MD và AB. a) Chứng minh: ∆CDM∾∆CAB. b) Chứng minh: MD.ME=MA.MC c) Chứng minh: 𝑀𝐴𝐷 ̂ = 𝑀𝐸𝐶 ̂ d) giả sử 𝑆𝐴𝐵𝐷𝑀 = 3𝑆𝐶𝐷𝑀, chứng minh: BC=2MC
Cho tam giác ABC nhọn, có hai đường cao BM và CN cắt nhau tại H.
a) CMR: AM. AC = AN. AB
b) Chứng minh hai tam giác AMN và ABC đồng dạng
c) Gọi P là giao điểm của AH với BC. CMR: PH là phân giác của góc MPN
d) Đường thẳng MN cắt BC tại D. CMR: DN. PM = DM. PN
Cho tam giác nhọn ABC, AH là đường cao. Gọi E,F lần lượt là hình chiếu của H trên cạnh AB và AC. Đường thẳng EF và BC cắt nhau tại D
a. chứng minh tam giác AFH đồng dạng tam giác AFC
b.chứng minh AH^2=AE.AB
c.chứng minh tam giác AEF đồng dạng tam giác ACB
d.Giả sử diện tích tam giacs EHF bằng ba lần diện tích tam giác DHE. tínhtỉ số HE/HF
Bổ Toán Bổ Đề Về Tính Chất Đường Phân Giác Trong Tam Giác Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của đoạn thẳng BC. Gọi D và E là hai điểm lần lượt thuộc AB và AC sao cho widehat{DME}widehat{ABC}a) Chứng minh rằng tam giác BMD đồng dạng với tam giác CEM.b) Chứng minh rằng DM là tia phân giác của góc widehat{BDE}.P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ!Em cám ơn nhiều ạ!
Đọc tiếp
Bổ Toán Bổ Đề Về Tính Chất Đường Phân Giác Trong Tam Giác
'' Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của đoạn thẳng BC. Gọi D và E là hai điểm lần lượt thuộc AB và AC sao cho \(\widehat{DME}=\widehat{ABC}\)
a) Chứng minh rằng tam giác BMD đồng dạng với tam giác CEM.
b) Chứng minh rằng DM là tia phân giác của góc \(\widehat{BDE}\).
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều ạ!










