Violympic toán 9
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A
Cmr ab/ab+bc=tanb
Cho tam giác ABC nhọn
Cmr cosa + cosb + cosc <= 3/2
Cho \(\Delta\)ABC đều. Chứng minh rằng: CosA+CosB+CosC=\(\frac{3}{2}\)
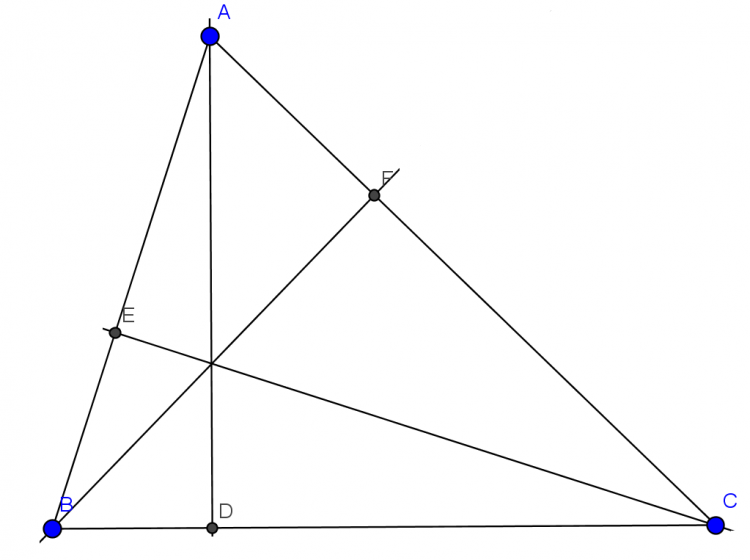
Cho tam giác ABC,vẽ 3 đường cao AD,BE,CF.CMR:
\(a)S_{AEF}=S_{ABC}.Cos^2A\\ b)AE.BF.CD=AB.AC.BC.CosA.CosB.CosC\\ c)\frac{S_{DEF}}{S_{ABC}}=1-\left(CosA-CosB-CosC\right)\)
Cho tam giác ABC có góc A là góc tù. Chứng minh rằng:
sin( B+C)= sinB .cosC+ cosB .sinC
Cho tam giác ABC nhọn. Chứng minh rằng: AB^2= AC^2+BC^2-2*AC*BC*cosC
Cho tam giác ABC nhọn . Cmr: AB2 = AC2 + BC2 - 2AC.BC. CosC
Cho tam giác ABC có 3 góc nhọn và các trung tuyến BM và CN vuông góc với nhau. Chứng minh: \(cotC+cotB\ge\dfrac{2}{3}\)
Cho tam giác ABC nhọn, đường BH và CK.
a) Hãy biểu thị cosA bằng 2 cách để chứng minh : ΔAHK ∼ ΔABC
b) Tính số đo góc A để diện tích ΔADE bằng diện tích tứ giác BCDE?
Cho tam giác ABC có ba góc nhọn và ABAC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.a) Chứng minh tứ giác BDHM nội tiếp đường tròn.b) Chứng minh DA là tia phân giác của widehat{MDC}c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.d) Chứng minh AB^2+AC^2+CD^2+BD^28R^2
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AB>AC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.
a) Chứng minh tứ giác BDHM nội tiếp đường tròn.
b) Chứng minh DA là tia phân giác của \(\widehat{MDC}\)
c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.
d) Chứng minh \(AB^2+AC^2+CD^2+BD^2=8R^2\)