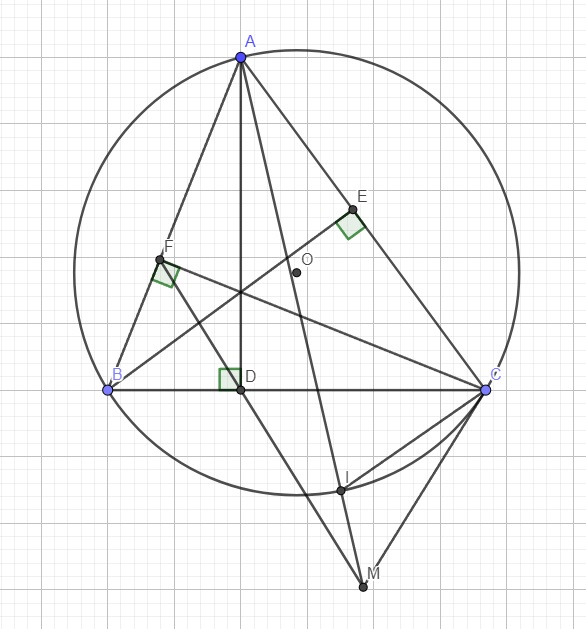
Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O).Các đường cao AD,BE,CF của tam giác ABC cắt nhau tại H.Tiếp tuyến tại C của đươnwgf tròn (o) cắt đường thẳng FD ở M
a)Chứng minh tứ giác ACDF nội típ đường tròn và tam giác CDM là tam giác cân
b)AM cắt đươngf tròn (O) tại I (I khác A),MD cắt BI tại N.Chứng minh:MC^2 =MI.MA
giup minh voi
a.
Theo giả thiết \(AD\perp BC\Rightarrow\widehat{ADC}=90^0\)
\(CF\perp AB\Rightarrow\widehat{AFC}=90^0\)
\(\Rightarrow\) F và D cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{BAC}+\widehat{CDF}=180^0\)
Mà \(\widehat{CDF}+\widehat{BDF}=180^0\) (kề bù)
\(\Rightarrow\widehat{BAC}=\widehat{BDF}\)
Lại có \(\widehat{BDF}=\widehat{MDC}\) (đối đỉnh)
\(\widehat{BAC}=\widehat{MCD}\) (góc nt và góc tiếp tuyến - dây cung cùng chắn AB)
\(\Rightarrow\widehat{MCD}=\widehat{MDC}\)
\(\Rightarrow\Delta CDM\) cân tại M
b.
Xét hai tam giác MCI và MAC có:
\(\left\{{}\begin{matrix}\widehat{CMI}-chung\\\widehat{MCI}=\widehat{CAI}\left(\text{cùng chắn CI}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MCI\sim\Delta MAC\left(g.g\right)\)
\(\Rightarrow\dfrac{MC}{MA}=\dfrac{MI}{MC}\Rightarrow MC^2=MI.MA\)