Question

Cho tam giác ABC (Hình 55), các điểm M, N thuộc cạnh AB thỏa mãn \(AM = MN = NB\), các điểm P, Q thuộc cạnh AC thỏa mãn \(AP = PQ = QC\). Tam giác AMP đồng dạng với những tam giác nào?

         

Answer 1

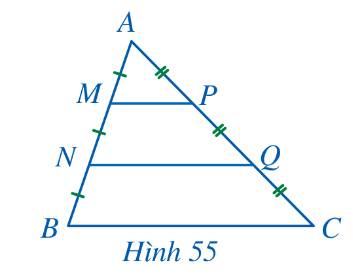
Vì \(AM = MN = NB\) và \(AP = PQ = QC\) nên M và P lần lượt là trung điểm của AN và AQ.

Khi đó MP là đường trung bình của tam giác ANQ.

\(\begin{array}{l} \Rightarrow MP//NQ\\ \Rightarrow \Delta AMP \backsim \Delta ANQ\\ \Rightarrow \widehat {AMP} = \widehat {ANQ}\end{array}\)

Ta có:

\(\frac{{AM}}{{AB}} = \frac{{AP}}{{AC}} = \frac{1}{3} \Rightarrow MP//BC\) (Định lý Thales đảo)

\( \Rightarrow \Delta AMP \backsim \Delta ABC\).