BC = BH + CH = 13 (cm)
∆ABH ~ ∆CAH (g.g)
=> AH² = BH . CH = 36
=> AH = 6
BM = 1/2 BC = 6,5 (cm)
=> HM = 2,5 (cm)
Do đó S_(AHM) = 1/2 . 2,5 . 6 = 7,5 (cm²)
1/ Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM
a/ Chứng minh AH2 = BH . CH
b/ Tính diện tích tam giác AMH , biết BH = 4cm , CH = 9cm
Tam giác vuông ABC (\(\widehat{A}=90^0\)) có đường cao AH và trung tuyến AM (h.36).
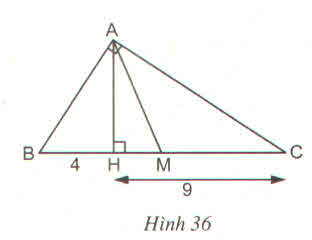
Tính diện tích tam giác AMH, biết BH = 4cm, CH = 9cm ?
1/ Cho tam giác ABC vuông tại C , đường cao CH ( H thuộc AB ). Biết AH = 4cm , BH = 9cm
a/ Chứng minh Tam giác ABC đồng dạng tam giác CBH
b/ Chứng minh BC bình phương = BH . BA
c/ Tính diện tích Tam giác ABC
Bài1. Cho tam giác ABC vuông tại A. Kẻ đường cao AH (H thuộc BC).
a) Tìm các cặp tam giác đồng dạng.
b) Chứng minh AH2=BH.CH; AB2 = BH.BC; AC2 = CH.BC
c) Biết BH=9cm, CH = 16cm. Tính độ dài các cạnh của tam giác ABC.
Mn giải giúp em với ạ em cảm ơn rất nhiều ạ 
Cho tam giác vuông góc tại A,đường cao AH, AB=15cm,BC=25cm,BH=9cm a.CM tam giác ABC đồng dạng tam giác HBA và AB.AH=BH.AC b.Phân giác của ^ABC cắt AH tại I, Tính AI và HI c.Phân giác của ^HAC cắt BC tại K. CM IK//AC (có gt kl giups em vs ạ)
Cho Tam giác ABC vuông tại A có AB=9cm, AC=12cm , đường cao AH a) chứng minh: tam giác abh ~ tam giác cba b) tính BC;AH c) Tia phân giác góc B cắt AC tại D.Chứng minh: AD.AC=AH.DC
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9 cm
Gọi D và E là hình chiếu của H trên AB và AC
a) Tính độ dài DE
b) Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N. Chứng minh M là trung điểm của BF, N là trung điểm của CH
c) Tính diện tích tứ giác DENM
