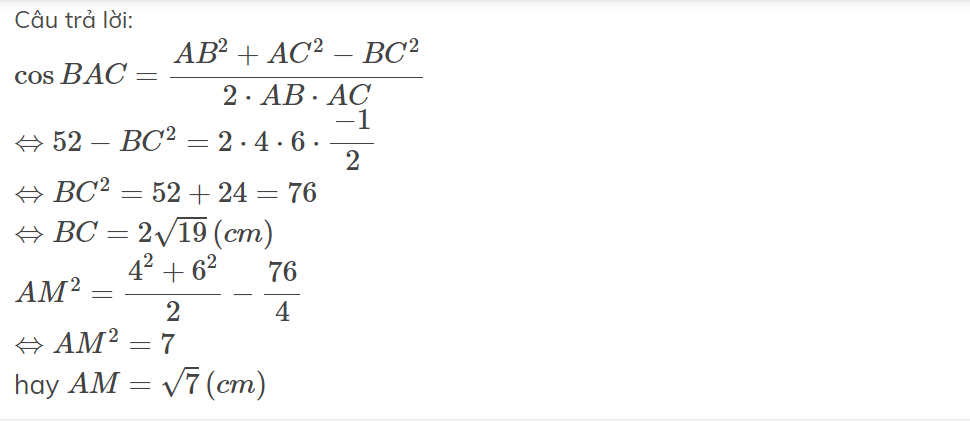Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Violympic toán 8
Các câu hỏi tương tự
Cho tam giác ABC có góc A bằng 120 độ; AB = 4 cm; AC = 6 cm. Trung tuyến AM (M thuộc BC). Tính AM
Cho tam giác ABC có góc A bằng 120 độ; AB = 4 cm; AC = 6 cm. Trung tuyến AM (M thuộc BC). Tính AM
cho tam giác ABC vuông tại A (ACAB), đường cao AH. Trên tia HD lấy điểm C sao cho HDHA. Đường vuông góc với BC tại D cắt AC tại E. 1) CMR: tam giác ADC và tam giác BEC đồng dạng. Tính độ dài đoạn BE theo ABm. 2) Gọi M là trung điểm của đoạn BE. CMR: tam giác BHM và tam giác BEC đồng dạng và HM vuông góc với AD. 3) Tia Am cắt BC tại G. CMR: GB/BCDH/AH+HC
Đọc tiếp
cho tam giác ABC vuông tại A (AC>AB), đường cao AH. Trên tia HD lấy điểm C sao cho HD=HA. Đường vuông góc với BC tại D cắt AC tại E.
1) CMR: tam giác ADC và tam giác BEC đồng dạng. Tính độ dài đoạn BE theo AB=m.
2) Gọi M là trung điểm của đoạn BE. CMR: tam giác BHM và tam giác BEC đồng dạng và HM vuông góc với AD.
3) Tia Am cắt BC tại G. CMR: GB/BC=DH/AH+HC
Cho tam giác ABC có AB=12cm , AC=15cm, BC=q6cm. Trên cạnh AB lấy điểm M sao cho AM=3cm. Từ M kẻ đường thẳng song song với BC cắt AC tại N, cắt trung tuyến AI tại K.
a/ Tính độ dài MN
b/ Chứng minh K là trung điểm của MN
c/ Trên tia MN lấy điểm P sao cho MP=8cm. Nối PI cắt AC tại Q. Chững minh tam giác QIC đồng dạng với tam giác AMN
Cho tam giác ABC đều, O là trung điểm của BC. M và N là các điểm trên AB và AC sao cho góc MON=60 độ. CM:
a) Tam giác OBM đồng dạng với tam giác NCO.
b) Tam giác OBM đồng dạng với tam giác NOM; MO là phân giác của góc BMN
c) O cách đều 3 cạnh AB, AC, MN
Cho tam giác ABC . Trên cạnh AB lấy điểm M . Trên cạnh AC lấy điểm N sao cho AM = 6 cm , BM = 4 cm , AN = 15 cm , CN = 10 cm
a, Chứng minh : MN // BC
b, Gọi K là trung điểm của BC , I là giao điểm của AK với MN . Chứng minh : I là trung điểm MN
Cho hình thang ABCd có AB = 4 cm ; CD = 6 cm và tổng góc C + góc D = 90 độ. Lấy M,N là trung điểm của AB, CD. tính MN
cho tam giác ABC vuông tại a có ah vuông góc với BC, trên cạnh AB, AC lấy 2 điểm E, D sao cho góc DHE=90 độ. Tìm vị trí của điểm D, E sao cho độ dài DE nhỏ nhất
Cho tam giác ABC vuông tại A có AC=4cm, trung tuyến AM. D là điểm đối xứng với M qua AB
a) CM: tứ giác AMBD là hình thoi
b) CM: CD đi qua trung điểm của AM
c) Tìm điều kiện của tam giác ABC để AMBD là hình vuông. Khi đó hãy tính \(S_{AMBD}\)