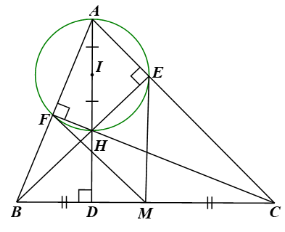
a) Vì BE, CF là đường cao của \(\Delta \)ABC nên \(BE \bot AC,CF \bot AB\)\( \Rightarrow \widehat {AEH} = \widehat {AFH} = \widehat {BFC} = \widehat {BEC} = {90^o}\)
Do đó, tam giác AFH vuông tại F và tam giác AEH vuông tại E.
Suy ra, bốn điểm A, E, H, F cùng thuộc đường tròn đường kính AH.
Mà I là trung điểm của AH nên tứ giác AEHF nội tiếp đường tròn tâm I.
b) Vì tứ giác AEHF nội tiếp đường tròn tâm I nên \(IA = IE\). Do đó, \(\Delta \)IAE cân tại I nên \(\widehat {IAE} = \widehat {IEA}\).
Lại có: \(\widehat {EAI} = \widehat {EBC}\) (cùng phụ với góc ACB) nên \(\widehat {IEA} = \widehat {EBC}\) (1)
\(\Delta \)BEC vuông tại E, EM là đường trung tuyến nên \(EM = MC\). Do đó, \(\Delta \)MEC cân tại M.
Suy ra, \(\widehat {MCE} = \widehat {MEC}\) (2)
\(\Delta \)BEC vuông tại E nên \(\widehat {ECB} + \widehat {EBC} = {90^o}\) (3)
Từ (1), (2) và (3) ta có: \(\widehat {MEC} + \widehat {IEA} = {90^o}\).
Mà \(\widehat {MEC} + \widehat {IEA} + \widehat {IEH} + \widehat {HEM} = {180^o} \Rightarrow \widehat {IEM} = {90^o}\). Do đó, \(IE \bot ME\) tại M. Mà E thuộc đường tròn ngoại tiếp tứ giác AEHF nên ME tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Chứng minh tương tự ta có: MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.


