Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.
a) Chứng minh rằng tam giác AMN là tam giác cân.
b) Kẻ BH ⊥ AM (H ∈AM), kẻ CK ⊥ AN (K∈AN). Chứng minh rằng BH = CK.
c) Chứng minh rằng AH = AK.
d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao ?
e) Khi góc BAC=60o và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và xác định dạnh của tam giác OBC.
a/ Ta có :
\(\Delta ABC\) cân tại A \(\left(gt\right)\Leftrightarrow\widehat{B_1}=\widehat{C_1}\left(t.c\Delta cân\right)\)
Lại có :
\(\left\{{}\begin{matrix}\widehat{B_1}+\widehat{B_2}=180^0\\\widehat{C_1}+\widehat{C_2}=180^0\end{matrix}\right.\)
\(\Leftrightarrow\widehat{B_2=C_2}\)
Xét \(\Delta ABM;\Delta ACN\) có :
\(\left\{{}\begin{matrix}BM=CN\\\widehat{B_2}=\widehat{C_2}\\AB=AC\end{matrix}\right.\) \(\Leftrightarrow\Delta ABM=\Delta ACN\left(c-g-c\right)\)
\(\Leftrightarrow AM=AN\)
\(\Leftrightarrow\Delta AMNcaan\)
a)Ta có:vì △ABC cân tại A)
nên ABM=ACN
Xét △ABM và △ACN có:
ABM=ACN (cmt)
AB=AC( vì △ABC cân tại A)
BM=CN (gt)
nên △ABM=△ACN(c-g-c)
do đó: M=N
vậy △AMN là tam giác cân và cân tại A
b)Xét △HMB vuông tại H và △KNC vuông tại K có:
M=N(cmt)
BM=CN(gt)
nên △HMB=△KNC(cạnh huyền-góc nhọn)
do đó:BH=CK
c)Xét △ABH vuông tại H và △ACK vuông tại K
AB=AC(vì △ABC cân tại A)
BH=CK(cmt)
nên △ABH=△ACK(cạnh huyền-cạnh góc vuông)
do đó:AH=AK
d)Xét △AOH vuông tại H và △AOK vuông tại K có:
AO là cạnh chung
AH=AK(cmt)
nên △AOH=△AOK(cạnh huyền-cạnh góc vuông)
do đó (góc) HAO=KAO
Gọi D là giao điểm của AO và MN
Xét △ADM và △ADN có:
AD là cạnh chung
Góc MAD=góc NAD(cmt)
AM=AN(vì AMN cân tại A)
nên △ADM=△ADN(c-g-c)
do đó:ADM=ADN
mà ADM+ADN=180o(hai góc kề bù)
suy ra:ADM=ADN=180o:2=90o
vậy AD ⊥MN.
Xét △ABD vuông tại D và △ACD vuông tại D có:
AB=AC(vì △ABC cân tại A)
ABD=ACD(vì △ABC cân tại A)
nên △ABD=△ACD(cạnh huyền-góc nhọn)
do đó:BAD=CAD
Xét △AOB và △AOC có:
AO là cạnh chung
AB=AC(vì △ABC cân tại A)
BAO=CAO(cmt)
nên △AOB=△AOC(c-g-c)
do đó OB=OC
Vậy △OBC là tam giác cân và cân tại O
_BL_:
Ta có hình vẽ :
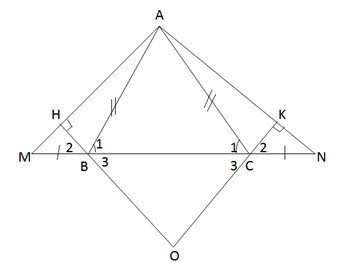
a) ∆ABC cân, suy ra góc B1= góc C1
⇒góc ABM= góc ACN
∆ABM và ∆CAN có:
AB = AC (gt)
góc ABM= góc ACN
BM = ON (gt)
Suy ra góc M=góc N
=>∆AMN là tam giác cân ở A.
Vậy ΔAMN cân tại A.
b) Hai tam giác vuông ∆BHM và ∆CKN có :
BM = CN (gt)
góc M=góc N (c/m từ câu a)
Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn)
Suy ra BH = CK.
Vậy BH=CK.
c) Theo câu (a) ta có ΔAMN cân ở A nên AM = AN (1)
Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (2).
Do đó AH = AM – HM = AN – KN (theo (1) và (2)) = AK
Vậy AH = AK.
d) ∆BHM = ∆CKN suy ra góc B2=góc C2
Mà góc B2=góc B3;góc C2=góc C3 (đối đỉnh)
Nên góc B3=góc C3.
=> ΔOBC cân tại O.
Vậy ∆OBC là tam giác cân.
e) Khi góc BAC=60o và BM = CN = BC.
+Tam giác cân ABC có góc BAC= 60o nên là tam giác đều.
Do đó: AB = BC = AC = BM = CN
góc ABM=góc ACN=120o (cùng bù với 600)
∆ABM cân ở B nên góc M=góc BAM =\(\dfrac{180^o-120^o}{2}=30^o\)
Suy ra góc ANM=góc AMN=30o.
Và góc MAN=180o− (góc AMN+ góc ANM)=180o−2.30o=120o.
Vậy ∆AMN có góc M=góc N=30o;góc A=120o.
+∆BHM có: góc M=30o nên góc B2=60 (hai góc phụ nhau)
Suy ra góc B3=60o
Tương tự góc C3=60o
Tam giác OBC có góc B3=góc C3=60o nên tam giác OBC là tam giác đều.
Vậy ΔOBC là Δ đều.
a) Do \(\bigtriangleup\)ABC là \(\bigtriangleup\)cân
=> \(B_1=C_1\)
AB = BC
Có: \(\widehat{ABM}\)+ \(B_1\) = \(180^0\)( 2 góc kề bù)
\(\widehat{ACN}\) + \(C_1\) = \(180^0\)(2 góc kề bù)
Mà \(B_1=C_1\)
=> \(\widehat{ABM}\) = \(\widehat{ACN}\)
Xét \(\bigtriangleup\)ABM và \(\bigtriangleup\)ACN, có: AB = AC
\(\widehat{ABM}\) = \(\widehat{ACN}\)
BM = CN
=>\(\bigtriangleup\)ABM = \(\bigtriangleup\)ACN ( c.g.c)
=>AM = AN( 2 cạnh tương ứng )
=> \(\bigtriangleup\)AMN cân tại A
b) Do \(\bigtriangleup\)ABM = \(\bigtriangleup\)ACN (theo câu a)
=> \(\widehat{BAM} \) = \(\widehat{CAN} \) (2 góc tương ứng)
Xét \(\bigtriangleup\) vuông ABH và \(\bigtriangleup\) vuông ACK, có: AB = AC
\(\widehat{BAM} \) = \(\widehat{CAN} \)
=> \(\bigtriangleup\) vuông ABH = \(\bigtriangleup\) vuông ACK (ch-gn)
=> BH = CK ( 2cạnh tương ứng )
c) Do \(\bigtriangleup\) vuông ABH = \(\bigtriangleup\) vuông ACK (c/m câu b)
=>AH = AK (2 cạnh tương ứng)
a)Ta có:vì △ABC cân tại A)
nên ABM=ACN
Xét △ABM và △ACN có:
ABM=ACN (cmt)
AB=AC( vì △ABC cân tại A)
BM=CN (gt)
nên △ABM=△ACN(c-g-c)
do đó: M=N
vậy △AMN là tam giác cân và cân tại A
b)Xét △HMB vuông tại H và △KNC vuông tại K có:
M=N(cmt)
BM=CN(gt)
nên △HMB=△KNC(cạnh huyền-góc nhọn)
do đó:BH=CK
c)Xét △ABH vuông tại H và △ACK vuông tại K
AB=AC(vì △ABC cân tại A)
BH=CK(cmt)
nên △ABH=△ACK(cạnh huyền-cạnh góc vuông)
do đó:AH=AK
d)Xét △AOH vuông tại H và △AOK vuông tại K có:
AO là cạnh chung
AH=AK(cmt)
nên △AOH=△AOK(cạnh huyền-cạnh góc vuông)
do đó (góc) HAO=KAO
Gọi D là giao điểm của AO và MN
Xét △ADM và △ADN có:
AD là cạnh chung
Góc MAD=góc NAD(cmt)
AM=AN(vì AMN cân tại A)
nên △ADM=△ADN(c-g-c)
do đó:ADM=ADN
mà ADM+ADN=180o(hai góc kề bù)
suy ra:ADM=ADN=180o:2=90o
vậy AD ⊥MN.
Xét △ABD vuông tại D và △ACD vuông tại D có:
AB=AC(vì △ABC cân tại A)
ABD=ACD(vì △ABC cân tại A)
nên △ABD=△ACD(cạnh huyền-góc nhọn)
do đó:BAD=CAD
Xét △AOB và △AOC có:
AO là cạnh chung
AB=AC(vì △ABC cân tại A)
BAO=CAO(cmt)
nên △AOB=△AOC(c-g-c)
do đó OB=OC
Vậy △OBC là tam giác cân và cân tại O
a) Ta có : góc ABC + góc ABM = 180o ( hai góc kề bù ) ; góc ACB + góc ACN = 180o ( hai góc kề bù ) mà góc ABC = góc ACB ( tam giác ABC cân tại A ) => góc ABM = góc ACN
Xét tam giác ABM và tam giác ACN ,có :
AB = AC ( gt )
góc ABM = góc ACN ( chứng minh trên )
BM = CN ( gt )
=> tam giác ABM = tam giác ACN ( c-g-c )
=> AM = AN ( hai cạnh tương ứng ) => tam giác AMN cân tại A
Vậy tam giác AMN cân tại A
b) Xét tam giác BHM và tam giác CKN ,có :
góc BHM = góc CKN ( = 90o )
BM = CN ( gt )
góc M = góc N ( tam giác AMN cân )
=> tam giác BHM = tam giác CKN ( ch - gn )
=> MH = NK ( hai cạnh tương ứng )
Ta có : AH + HM = AM ; AK + KN = AN mà HM = NK => AH = AK
Vậy AH = AK
c) Vì tam giác BHM = tam giác CKN ( chứng minh trên ) => góc HBM = góc KCN ( hai góc tương ứng ) mà góc KCN = góc BCO ( đối đỉnh ) ; góc HBM = góc CBO ( đối đỉnh ) => góc BCO = góc CBO => tam giác OBC cân tại O
Vậy tam giác OBC là tam giác cân
e)
a)Ta có:vì △ABC cân tại A)
nên ABM=ACN
Xét △ABM và △ACN có:
ABM=ACN (cmt)
AB=AC( vì △ABC cân tại A)
BM=CN (gt)
nên △ABM=△ACN(c-g-c)
do đó: M=N
vậy △AMN là tam giác cân và cân tại A
b)Xét △HMB vuông tại H và △KNC vuông tại K có:
M=N(cmt)
BM=CN(gt)
nên △HMB=△KNC(cạnh huyền-góc nhọn)
do đó:BH=CK
c)Xét △ABH vuông tại H và △ACK vuông tại K
AB=AC(vì △ABC cân tại A)
BH=CK(cmt)
nên △ABH=△ACK(cạnh huyền-cạnh góc vuông)
do đó:AH=AK
d)Xét △AOH vuông tại H và △AOK vuông tại K có:
AO là cạnh chung
AH=AK(cmt)
nên △AOH=△AOK(cạnh huyền-cạnh góc vuông)
do đó (góc) HAO=KAO
Gọi D là giao điểm của AO và MN
Xét △ADM và △ADN có:
AD là cạnh chung
Góc MAD=góc NAD(cmt)
AM=AN(vì AMN cân tại A)
nên △ADM=△ADN(c-g-c)
do đó:ADM=ADN
mà ADM+ADN=180o(hai góc kề bù)
suy ra:ADM=ADN=180o:2=90o
vậy AD ⊥MN.
Xét △ABD vuông tại D và △ACD vuông tại D có:
AB=AC(vì △ABC cân tại A)
ABD=ACD(vì △ABC cân tại A)
nên △ABD=△ACD(cạnh huyền-góc nhọn)
do đó:BAD=CAD
Xét △AOB và △AOC có:
AO là cạnh chung
AB=AC(vì △ABC cân tại A)
BAO=CAO(cmt)
nên △AOB=△AOC(c-g-c)
do đó OB=OC
Vậy △OBC là tam giác cân và cân tại O
a/ Ta có :
cân tại A (gt)⇔ˆB1=ˆC1(t.cΔcân)(gt)⇔B1^=C1^(t.cΔcân)
Lại có :
{ˆB1+ˆB2=1800ˆC1+ˆC2=1800{B1^+B2^=1800C1^+C2^=1800
⇔ˆB2=C2⇔B2=C2^
Xét ΔABM;ΔACNΔABM;ΔACN có :
⎧⎪⎨⎪⎩BM=CNˆB2=ˆC2AB=AC{BM=CNB2^=C2^AB=AC ⇔ΔABM=ΔACN(c−g−c)⇔ΔABM=ΔACN(c−g−c)
⇔AM=AN⇔AM=AN
⇔ΔAMNcaan
a)Ta có:vì △ABC cân tại A)
nên ABM=ACN
Xét △ABM và △ACN có:
ABM=ACN (cmt)
AB=AC( vì △ABC cân tại A)
BM=CN (gt)
nên △ABM=△ACN(c-g-c)
do đó: M=N
vậy △AMN là tam giác cân và cân tại A
b)Xét △HMB vuông tại H và △KNC vuông tại K có:
M=N(cmt)
BM=CN(gt)
nên △HMB=△KNC(cạnh huyền-góc nhọn)
do đó:BH=CK
c)Xét △ABH vuông tại H và △ACK vuông tại K
AB=AC(vì △ABC cân tại A)
BH=CK(cmt)
nên △ABH=△ACK(cạnh huyền-cạnh góc vuông)
do đó:AH=AK
d)Xét △AOH vuông tại H và △AOK vuông tại K có:
AO là cạnh chung
AH=AK(cmt)
nên △AOH=△AOK(cạnh huyền-cạnh góc vuông)
do đó (góc) HAO=KAO
Gọi D là giao điểm của AO và MN
Xét △ADM và △ADN có:
AD là cạnh chung
Góc MAD=góc NAD(cmt)
AM=AN(vì AMN cân tại A)
nên △ADM=△ADN(c-g-c)
do đó:ADM=ADN
mà ADM+ADN=180o(hai góc kề bù)
suy ra:ADM=ADN=180o:2=90o
vậy AD ⊥MN.
Xét △ABD vuông tại D và △ACD vuông tại D có:
AB=AC(vì △ABC cân tại A)
ABD=ACD(vì △ABC cân tại A)
nên △ABD=△ACD(cạnh huyền-góc nhọn)
do đó:BAD=CAD
Xét △AOB và △AOC có:
AO là cạnh chung
AB=AC(vì △ABC cân tại A)
BAO=CAO(cmt)
nên △AOB=△AOC(c-g-c)
do đó OB=OC
Vậy △OBC là tam giác cân và cân tại O
a)Ta có:vì △ABC cân tại A)
nên gócABM=góc ACN
Xét △ABM và △ACN có:
ABM=ACN (cmt)
AB=AC( vì △ABC cân tại A)
BM=CN (gt)
nên △ABM=△ACN(c-g-c)
do đó: M=N
vậy △AMN là tam giác cân và cân tại A
b)Xét △HMB vuông tại H và △KNC vuông tại K có:
M=N(cmt)
BM=CN(gt)
nên △HMB=△KNC(cạnh huyền-góc nhọn)
do đó:BH=CK
c)Xét △ABH vuông tại H và △ACK vuông tại K
AB=AC(vì △ABC cân tại A)
BH=CK(cmt)
nên △ABH=△ACK(cạnh huyền-cạnh góc vuông)
do đó:AH=AK
d)Xét △AOH vuông tại H và △AOK vuông tại K có:
AO là cạnh chung
AH=AK(cmt)
nên △AOH=△AOK(cạnh huyền-cạnh góc vuông)
do đó góc HAO=góc KAO
Gọi D là giao điểm của AO và MN
Xét △ADM và △ADN có:
AD là cạnh chung
Góc MAD=góc NAD(cmt)
AM=AN(vì AMN cân tại A)
nên △ADM=△ADN(c-g-c)
do đó:góc ADM=góc ADN
mà ADM+ADN=180o(hai góc kề bù)
suy ra:ADM=ADN=180o:2=90o
vậy AD ⊥MN.
Xét △ABD vuông tại D có:
AB=AC(vì △ABC cân tại A)
góc ABD=góc ACD(vì △ABC cân tại A)
nên △ABD=△ACD(cạnh huyền-góc nhọn)
do đó:góc BAD=góc CAD
Xét △AOB và △AOC có:
AO là cạnh chung
AB=AC(vì △ABC cân tại A)
gócBAO= gócCAO(cmt)
nên △AOB=△AOC(c-g-c)
do đó OB=OC
Vậy △OBC là tam giác cân và cân tại O


















