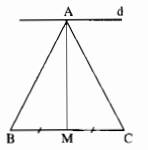
∆ABC cân tại A, AM là đường trung tuyến nên AM cũng là đường cao.
AM⊥BC
d⊥AM(gt)
Suy ra: d // BC (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba).

∆ABC cân tại A, AM là đường trung tuyến nên AM cũng là đường cao.
AM⊥BC
d⊥AM(gt)
Suy ra: d // BC (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba).
Cho ∆abc vuông tại a có ab=6cm, ac=8cm. Tia phân giác của góc abc cắt ac tại d.
a)Tính bc
b) Kẻ ah vuông góc với bc, tia ah cắt bc tại k. Chứng minh:∆ahb=∆khb
c) Chứng minh:dk vuông góc với bc
d) Qua c kẻ đường thẳng song song với ak, cắt tia ba tại e. Chứng minh:2(ad+ae)>ec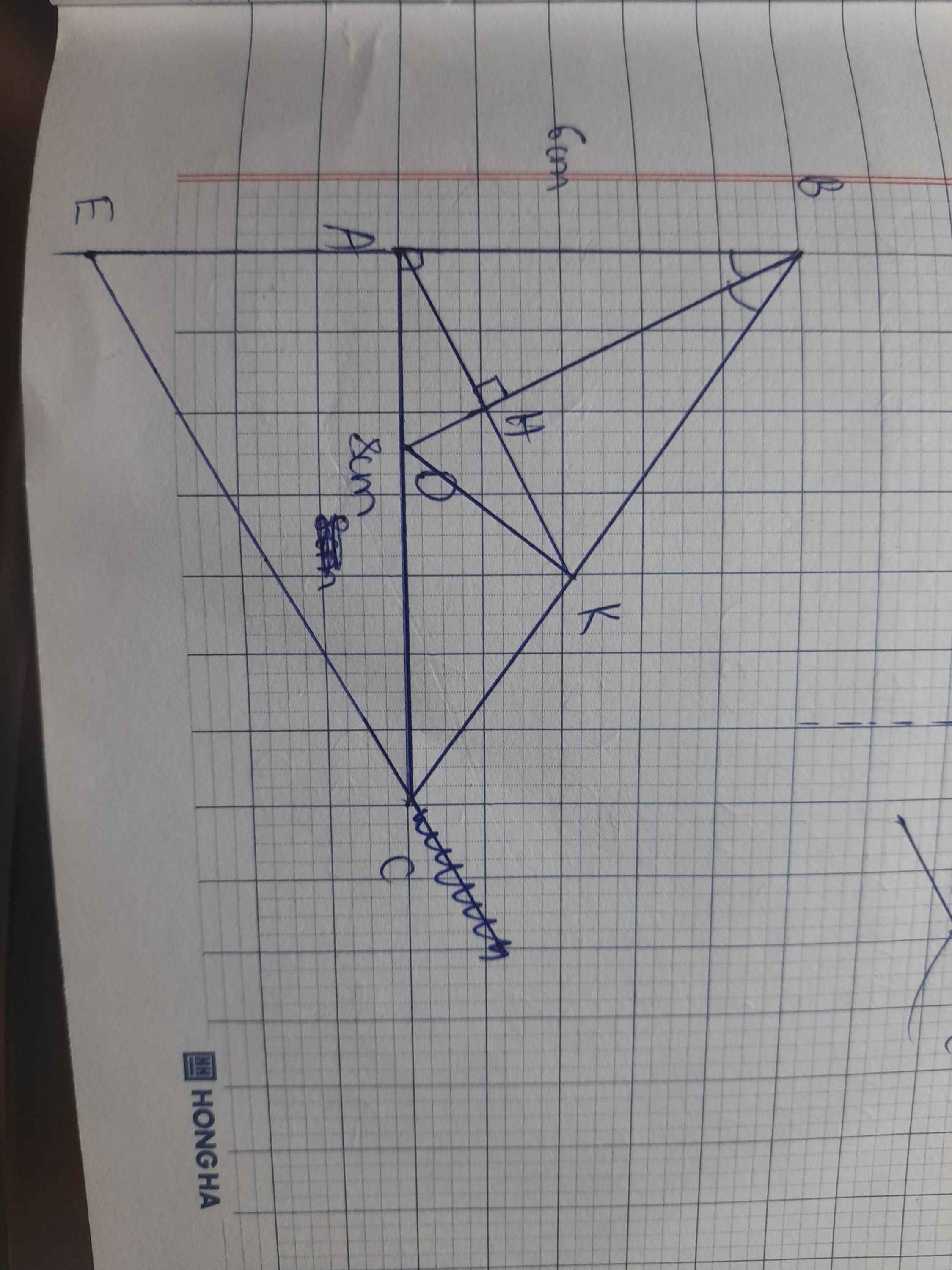
cho tam giác abc vuông tại a kẻ đường cao ah lấy điểm k thuộc doạn thẳng hc qua k kẻ đường thắngong song với ab cắt ah tại d chứng minh ak vuông góc cd
tam giác ABC vuông tại A trên cạnh AC lấy D bất kỳ.Qua D kẻ đường thẳng vuông góc với BC tại E: từ C kẻ đường thẳng vuông góc với BD tại F: chứng minh AB,CF,DE cùng đi qua 1 điểm
Cho tam giác ABC cân tại A . AI là đường trung tuyến. Chứng minh ∆ABI=∆ACI. Kẻ IN song song AB chứng minh NA=NC
Cho tam giác ABC vuông tại A kẻ phân giác BD của góc ABC từ d kẻ DE vuông góc với BC tại E a) Chứng minh tam giác BEA cân b) Chứng minh DB là trung trực của AE c) Chứng minh DA
Bài 2. Cho tam giác ABc cân tại A có đường trung tuyến AM, đường cao BE. Trên tia BA lấy điểm F sao cho BF = CE.
a)Chứng minh ΔBFC = ΔCEB
b) Chứng minh ba đường thẳng BE, CF, AM đồng quy
Bài 2. Cho tam giác ABc cân tại A có đường trung tuyến AM, đường cao BE. Trên tia BA lấy điểm F sao cho BF = CE.
a)Chứng minh ΔBFC = ΔCEB
b) Chứng minh ba đường thẳng BE, CF, AM đồng quy
Bài 2. Cho tam giác ABc cân tại A có đường trung tuyến AM, đường cao BE. Trên tia BA lấy điểm F sao cho BF = CE.
a)Chứng minh ΔBFC = ΔCEB
b) Chứng minh ba đường thẳng BE, CF, AM đồng quy
Cho tam giác DEF cân tại D với đường trung tuyến DI
a) chứng minh tam giác DEI=tam giác DFI
b)chứng minhDI vuông góc EF