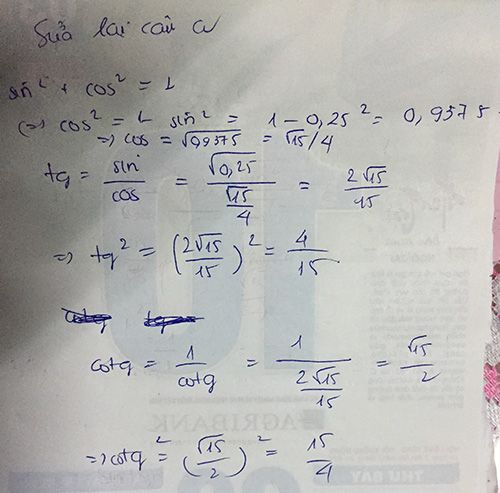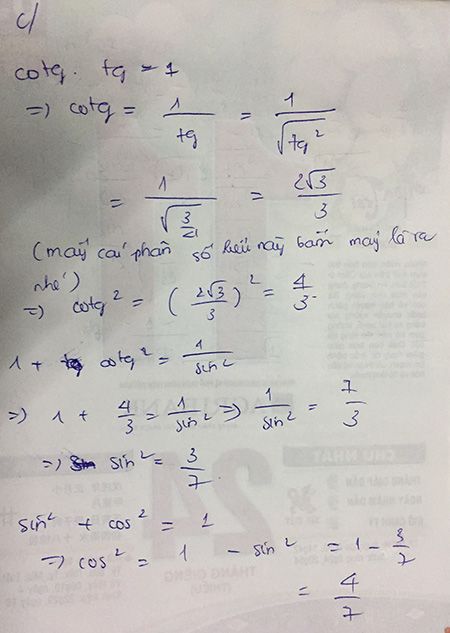Ôn tập Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
1/ Cho \(\sin\alpha=0,28.\)Tính \(\cos\alpha\), tg\(\alpha\), cotg\(\alpha\)
2/ Cho góc nhọn \(\alpha\). chứng minh rằng: \(1-2\cos^2\alpha=\sin^4\alpha-\cos^4\alpha\)
Cho tg a=7/24. Tính sin a, cos a, cotg a.
1. Cho cotg\(\alpha\)=5. Tính giá trị của biểu thức : \(\dfrac{\sin\alpha+\cos\alpha}{\sin\alpha-\cos\alpha}\)
2. Cho tam giác ABC vuông tại A có AC=4cm, AB+BC=8cm. Tính \(tg\dfrac{B}{2}\)
Hãy đơn giản biểu thức :
a) 1-sin^2alpha
b) sin^4alpha+cos^4alpha+2sin^2alphacos^2alpha
c) left(1-cosalpharight)left(1+cosalpharight)
d) tg^2alpha-sin^2alpha.tg^2alpha
e) 1+sin^2alpha+cos^2alpha
g) cos^2alpha+tg^2alpha.cos^2alpha
h) sinalpha-sinalpha.cos^2alpha
i) tg^2alphaleft(2cos^2alpha+sin^2alpha-1right)
Đọc tiếp
Hãy đơn giản biểu thức :
a) \(1-\sin^2\alpha\)
b) \(\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha\cos^2\alpha\)
c) \(\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)\)
d) \(tg^2\alpha-\sin^2\alpha.tg^2\alpha\)
e) \(1+\sin^2\alpha+\cos^2\alpha\)
g) \(\cos^2\alpha+tg^2\alpha.\cos^2\alpha\)
h) \(\sin\alpha-\sin\alpha.\cos^2\alpha\)
i) \(tg^2\alpha\left(2\cos^2\alpha+\sin^2\alpha-1\right)\)
Trong hình 44, hệ thức nào trong các hệ thức sau là đúng ?
(A) sinalphadfrac{b}{c} (B) cotgalphadfrac{b}{c} (C) tgalphadfrac{a}{c} (D) cotgalphadfrac{a}{c}
b) Trong hình 45, hệ thức nào trong các hệ thức sau không đúng ?
(A) sin^2alpha+cos^2alpha1
(B) sinalphacosbeta
(C) cosbetasinleft(90^0-alpharight)
(D) tgalphadfrac{sinalpha}{cosalpha}
Đọc tiếp
Trong hình 44, hệ thức nào trong các hệ thức sau là đúng ?
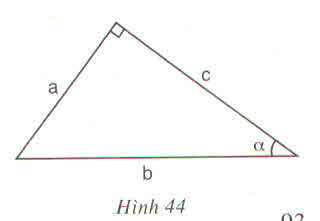
(A) \(\sin\alpha=\dfrac{b}{c}\) (B) \(cotg\alpha=\dfrac{b}{c}\) (C) \(tg\alpha=\dfrac{a}{c}\) (D) \(cotg\alpha=\dfrac{a}{c}\)
b) Trong hình 45, hệ thức nào trong các hệ thức sau không đúng ?
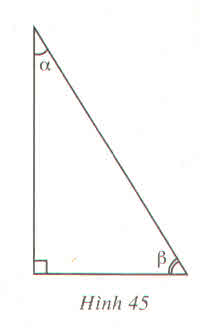
(A) \(\sin^2\alpha+\cos^2\alpha=1\)
(B) \(\sin\alpha=\cos\beta\)
(C) \(\cos\beta=\sin\left(90^0-\alpha\right)\)
(D) \(tg\alpha=\dfrac{\sin\alpha}{\cos\alpha}\)
a, bt sin α=3/5, tính A= 5 \(sin^2\)α + 6\(cos^2\)α.
b,bt cos α= 4/5, tính B= 4\(sin^2\)α - 5\(cos^2\)α.
Hãy tính biểu thức sau:
A= 2. Sin 30°- 2. Cos 60°+Tg 45°
2, chứng minh
a, ( 1- cos a ) ( 1+ cos a) = \(^{sin^2}\) a
b, 1+ \(sin^2\) a + \(cos^2\) a =2
c, sin a - sin a . \(cos^2\) a = \(sin^3\) a
d, \(sin^4\) + \(cos^4\) a + 2\(sin^2\)
cho tam giác abc có 3 góc nhọn. Vẽ đường cáo AD, BE, CF cắt nhau tại H. Chứng minh:
a) \(0< cos^2A+cos^2B+cos^2C< 1\)
b)\(2< sin^2A+sin^2B+sin^2C< 3\)
c)sinA + sinB + sinC < 2( cosA + cosB + cosC)
d)sinB . cosC + sinC . cosB = sinA
e)tanA + tanB + tanC = tanA . tanB . tanC