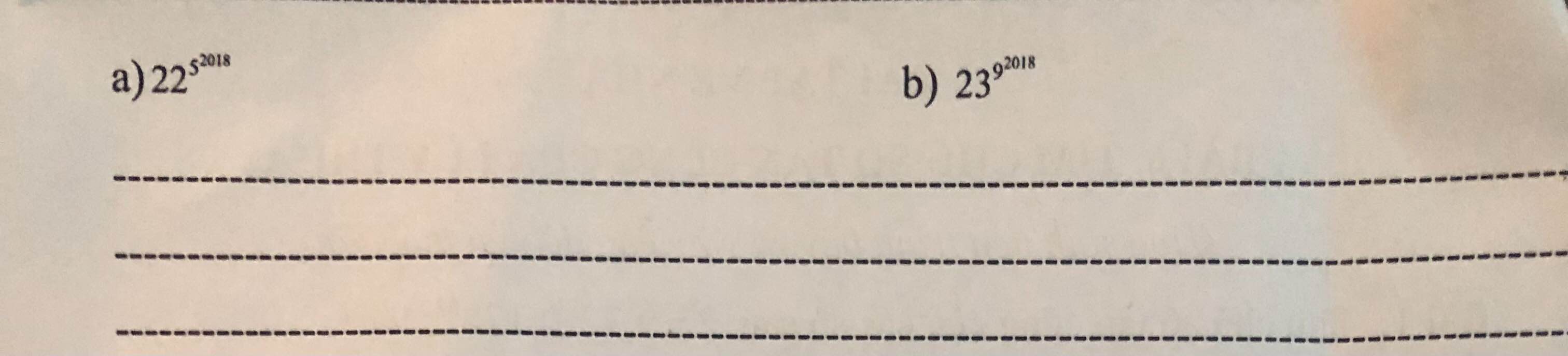\(S=3+3^2+...+3^{100}\)
\(\Leftrightarrow3S=3^2+3^3+...+3^{100}+3^{101}\)
\(\Rightarrow2S=3^{101}-3\)
Ta có \(3^{101}=3^{4.25+1}\Rightarrow3^{101}\) có tận cùng là 3
\(\Rightarrow3^{101}-3\) có tận cùng là 0
\(\Rightarrow S\) có tận cùng là 5
S=3+32+...+3100S=3+32+...+3100
⇔3S=32+33+...+3100+3101⇔3S=32+33+...+3100+3101
⇒2S=3101−3⇒2S=3101−3
Ta có có tận cùng là 3
có tận cùng là 0
có tận cùng là 5