xét tam giác abc vg tại a
AB^2=BC^2-AC^2=36
AB=6 cm
ta có AE/AC=EB/BC
AE+EB/AC+BC=AB/AC+BC
thay số 6/18=1/3
AE=1/3*8=2,6
EB=1/3*10=3,3
Đúng 1
Bình luận (2)
Bài 3: Tính chất đường phân giác của tam giác
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Gọi BD là đường phân giác của tam giác ABC.
a) Tính độ dài DA, DC.
b) Tia phân giác của góc C cắt BD tại I. Gọi M là trung điểm của BC. Chứng minh \(\widehat{BIM}\) = 90o
Cho tam giác ABC vuông tại A biết AB=6cm BC=10cm BM là đường phân giác góc B
Tính AM=?
Xem chi tiết
Tam giác ABC có AB = 5cm, AC = 6cm và BC = 7cm. Tia phân giác của góc BAC cắt cạnh BC tại E. Tính các đoạn EB, EC ?
Cho tam giác abc có AB=16cm Ac=32cm BC=21cm. Đường phân giác trong vài ngoài của góc A cắt BC lần lượt tại D và E. a) Cm B là trung điểm của EC b) Tính DE
20 tháng 2 2022 lúc 9:35
Bài 1: Cho tam giác abc có AB = 5cm AC = 7cm BC = 9cm. Đường phân giác AD. Tính DB, DC
Bài 2: Cho tam giác ABC vuông tại A. AB = 6cm, AC = 8cm, phân giác AD. Tính DB, DC
Cho tam giác ABC vuông tại A (AB < AC), kẻ đường cao AH, đường trung tuyến AM. Đường thẳng vuông góc với AM tại A cắt đường thẳng BC tại D. Chứng minh rằng:
a) AB là tia phân giác của góc DAH.
b) BH.CD = BD.CH
Cho tam giác cân ABC (AB = AC), đường phân giác góc B cắt AC tại D và cho biết AB = 15 cm, BC = 10 cm (h.19)
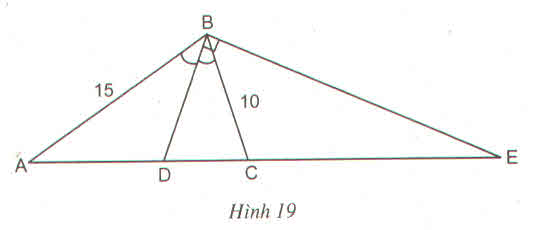
a) Tính AD, DC
b) Đường vuông góc với BD tại B cắt đường thẳng AC kéo dài tại E. Tính EC
Cho tam giác ABC vuông tại A (AB < AC), kẻ đường cao AH, đường trung tuyến AM. Đường thẳng vuông góc với AM tại A cắt đường thẳng BC tại D. Chứng minh rằng: a) AB là tia phân giác của góc DAH. b) BH.CD = BD.CH
cho ABCD là hình thang cân (AB//CD,AB<CD,góc ADC=60 độ),đường phân giác của góc ADC cắt AC,AB lần lượt tại I,M.Kẻ AE//BC(E thuộc DC).
a) chứng minh tam giác ADE là tam giác đều và DC=AB+AM.
b)Cho IA/IC=4/11 và MA-MB=6cm.Tính MB/AM và AM,MB.