Chương I - Căn bậc hai. Căn bậc ba
Các câu hỏi tương tự
Cho x,y,z>0 và xy+yz+zx=9. Tìm MaxP=x^5/y^3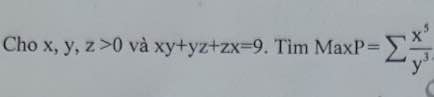
Cho x,y,z > 0 thỏa mãn : x + y + z = 2
Tìm GTNN của \(P=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
cho ba số x,y,z thỏa mãn đồng thời :\(\left\{{}\begin{matrix}x-2\sqrt{y}+1=0\\y-2\sqrt{z}+1=0\\z-2\sqrt{x}+1=0\end{matrix}\right.\)
tính giá trị của biểu thức A= x1000 +y1000+z1000
Cho x, y, z > 0 thỏa mãn \(x+y+z\le3\).Tìm GTLN :
\(A=\sqrt{1+x^2}+\sqrt{1+y^2}+\sqrt{1+z^2}+2\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)\)
Cho x,y,z>0 thỏa mãn xyz=1. Tìm min \(P=\dfrac{x^2\left(y+z\right)}{y\sqrt{y}+2z\sqrt{z}}+\dfrac{y^2\left(z+x\right)}{z\sqrt{z}+2x\sqrt{x}}+\dfrac{z^2\left(x+y\right)}{x\sqrt{x}+2y\sqrt{y}}\)
cho a, b, c, x, y, z là các số thực. thỏa mãn: a, b, c #0, x+y+z=0, \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=0\)
tính: \(Q=a^2x+b^2y+c^2z\)
Cho x,y,z >0 t/m \(x+y+z\ge12\). Tìm GTNN của
\(P=\dfrac{x}{\sqrt{y}}+\dfrac{y}{\sqrt{z}}+\dfrac{z}{\sqrt{x}}\)
cho xyz khác 0 thỏa mãn x^3+y^3+z^3=x^5+y^5+z^5.tính S=x^2+y^2+z^2
Cho các số x, y, z > 0 thỏa mãn x + y + z = 1. Tìm GTLN của biểu thức:
\(A=\frac{x}{9x^3+3y^2+z}+\frac{y}{9y^3+3z^2+x}+\frac{z}{9z^3+3x^2+y}+2017\left(xy+yz+zx\right)\)
Cho x, y, z > 0 thỏa mãn x + y +z = xy + yz + zx
CMR \(\frac{1}{x^2+y+1}+\frac{1}{y^2+z+1}+\frac{1}{z^2+x+1}\le1\)










