Ôn tập: Tam giác đồng dạng
Các câu hỏi tương tự
cho tam giác MNP vuông tại M phân giác ND đường cao MH
a)chứng minh tam giác MNP đồng dạng tam giác AMP
b) biết MN=6cm;NP=10cm tính MP;DP
Bài 4: Cho tam giác ABC vuông tại A đường cao AH . a) Chứng minh tam giác AHB đồng dạng tam giác ABC b) Gọi M , N lần lượt là trung điểm của BC và AB . Đường vuông góc BC kẻ từ B cắt MN tại I . Chứng minh c) IC cắt AH tại O . Chứng minh O là trung điểm AH d) Gọi K là giao điểm của CA và BI . Tính độ dài BK ,biết AB 15 cm , AC 20 cm .
Đọc tiếp
Bài 4: Cho tam giác ABC vuông tại A đường cao AH .
a) Chứng minh tam giác AHB đồng dạng tam giác ABC
b) Gọi M , N lần lượt là trung điểm của BC và AB . Đường vuông góc BC kẻ từ B cắt MN tại I . Chứng minh
c) IC cắt AH tại O . Chứng minh O là trung điểm AH
d) Gọi K là giao điểm của CA và BI . Tính độ dài BK ,biết AB = 15 cm , AC = 20 cm .
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC ) kẻ HD vuông góc với AC tại D (D thuộc AC) . a) Chứng minh: ADAH đồng dạng với AHAC từ đó suy ra A * H ^ 2 AD.AC b) Từ A vẽ đường phân giác của góc HAC cắt HD, BC lần lượt tại I và K. Chứng minh: AH .AIAD.AK và AHIK cân. c) Từ C vẽ CJ vuông góc với AK (J in AK ). Chứng minh: A * K ^ 2 AH.AC-HK.KCgiúp mình giải câu C nhé15:25 Đã gửi
Đọc tiếp
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC ) kẻ HD vuông góc với AC tại D (D thuộc AC) . a) Chứng minh: ADAH đồng dạng với AHAC từ đó suy ra A * H ^ 2 =AD.AC b) Từ A vẽ đường phân giác của góc HAC cắt HD, BC lần lượt tại I và K. Chứng minh: AH .AI=AD.AK và AHIK cân. c) Từ C vẽ CJ vuông góc với AK (J in AK ). Chứng minh: A * K ^ 2 =AH.AC-HK.KCgiúp mình giải câu C nhé15:25 Đã gửi
Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm.Từ B kẻ đường thẳng // với AC;phân giác góc BAC cắt BC tại M và cắt đường thẳng AB tại N a ) Chứng mình tam giác BMN đồng dạng với tam giác CMA b ) chứng minh AB/AC=MN/AN C) từ N kẻ NE vuông góc với AC (E thuộc AC) NE cắt BC tại I tính BI
Cho tam giác MNP cân tại M .Vẽ 3 đường cao MP,ME,PF ( D thuộc NP)(E thuộc MP)(F thuộc MN) a) chứng minh tam giác DMP đồng dạng với tâm giác ENP b) cho NP = 12cm , MP = 18cm . Tính độ dài PE
tam giác MNP vuông tại M, MN = 36, MP = 48 cm ,tia phân giác MK .tia phân giác của góc N cắt MK tại H .qua H kẻ đường thẳng song song với NP, cắt MN và MP ở d và e
a, tính độ dài NK
b, tính tỉ số MH/MK
c, tính DE
tam giác MNP vuông tại M, MN = 36, MP = 48 cm ,tia phân giác MK .tia phân giác của góc N cắt MK tại H .qua H kẻ đường thẳng song song với NP, cắt MN và MP ở d và e
a, tính độ dài NK
b, tính tỉ số MH/MK
c, tính DE
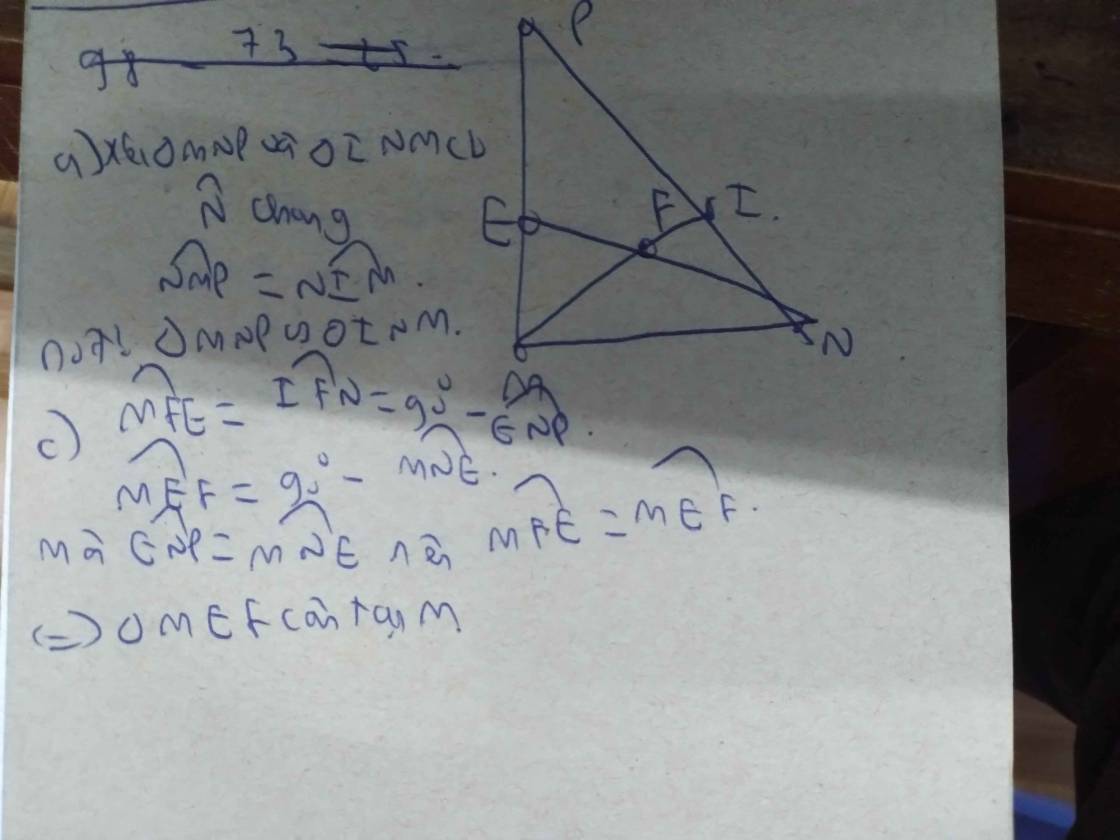
Cho hình chữ nhật MNPQ (MN > NP). MH vuông góc với QN tại H.
a) Chứng minh các tam giác MNH và NQP đồng dạng.
b) Chứng minh QN . NH = MN2
c) Lấy E, F lần lượt là trung điểm của NH, MH. Chứng minh tam giác MNE đồng dạng với tam giác QMF.
d) MH cắt PQ tại I. Tính diện tích tam giác MNI, biết QI = \(\dfrac{1}{2}\)IP và diện tích tam giác QHI là 3cm2
Mọi người ơi làm giúp mình bài này với ạ
Cho tam giác ABC nhọn(AB<AC) có 2 đường cao BD và CE cắt nhau tại H.
1.Chứng minh tam giác ABD đồng dạng với tam giác ACE
2. Chứng minh HD.HB= HC.HE
3.AH cắt BC tại F. Kẻ FI vuông góc với AC tại I. Chứng minh IF/IC=FA/CF
4. Trên tia đối của AF lấy điểm N sao cho AN=AF. Gọi M là trung điểmcủa cạnh IC. Chứng minh NI=FM.