Cho mặt phẳng (P1):
2x + 2y + 2z + 1 = 0 (1)
và mặt phẳng (P2):
x + y + z – 1 = 0 (2)
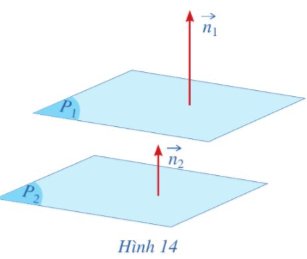
a) Gọi \(\overrightarrow{n_1}=\left(2;2;2\right),\overrightarrow{n_2}=\left(1;1;1\right)\) lần lượt là vectơ pháp tuyến của hai mặt phẳng (P1), (P2) (Hình 14). Tìm liên hệ giữa \(\overrightarrow{n_1}\) và \(2\overrightarrow{n_2}\).
b) Tìm các hệ số tự do D1, D2 lần lượt trong hai phương trình (1), (2). So sánh D1 và 2D2.
c) Nêu vị trí tương đối của hai mặt phẳng (P1), (P2).